physics0523's 精進ログ

主に競プロの面白い問題の解法をメモします

Double Clique (NAIPC2018-B)

https://www.acmicpc.net/problem/16041

$N$ 頂点 $M $ 辺のグラフ $G$ が与えられる。

頂点の部分集合 $S$ であって以下の条件を満たすものを $\mod 10^9+7$ で求めよ。

  • $S$ から誘導される部分グラフは完全グラフである。
  • 頂点全体の集合を $V$ としたとき、 $V \setminus S$ から誘導されるグラフに辺はない(補グラフが完全グラフである)。

$1 \le N,M \le 2 \times 10^5$

 

まず、 $\mod 10^9+7$ はこけおどし。実は $O(N)$ 個しかない。(自分が公式の実装例を読解している時、これを知ってもあまり方針がピンと来ませんでしたが…)

ここで、ある $S$ の取り方を吟味しよう。

実は、次の事柄が成り立つ。

  • ある valid な取り方で $|S|=k$ となったとき、 valid な取り方でありうる $|S|$ は $k- 1,k,k+1$ のみである。

証明:

今の $S$ から $2$ 頂点以上を $V \setminus S$ 側に動かすことは許されない。逆に、今の $V \setminus S$ から $2$ 頂点以上を $S$ 側に動かすことも許されない。

ここから、 valid な取り方として考えられるサイズは高々 $2$ つの連続する整数であるということも言える。 

 

さらに、常に次の事柄も成り立つ。

  • $S$ 中の頂点 $u$ 、 $V \setminus S$ 中の頂点 $v$ を好きに選ぶ。
  • この時、 $u,v$ をどう選んでも ( $u$ の次数 ) $\ge$ ( $v$ の次数 ) が成り立つ。

証明:

まず、 ( $u$ の次数 ) $\ge |S|-1$ 、 ( $v$ の次数 ) $\le |S|$ である。

これは、「 $u$ から $S$ 中の他の頂点全てに辺が伸びている必要がある」「 $v$ から辺が伸びて良いのは $S$ 中の頂点のみである」ことから言える。

ここで、 ( $u$ の次数 ) $= |S|-1$ 、 ( $v$ の次数 ) $= |S|$ なるケースがあるとマズい。このような場合 $v$ から $S$ 中の全てに辺が伸びている必要がある。しかし、 ( $u$ の次数 ) は $|S|-1$ であるので $S$ に含まれない頂点に辺を伸ばす余裕はない。よって、このようなことは起きないことが言えた。

 

次に、この等号成立条件を吟味する。

等号が成立する場合、先ほどの 頂点 $v$ から少なくとも $|S|-1$ 辺の辺が伸びている必要がある。これを以下の $2$ 通りに場合分けする。

  • $v$ から丁度 $|S|$ 辺伸びている場合
    • $S$ に $v$ を付け加えても valid な取り方である。
  • $v$ から丁度 $|S|-1$ 辺伸びている場合
    • $v$ から辺が伸びていない頂点 $w$ が $S$ 中にただ一つ存在する。このとき、 $v$ と $w$ を入れ替えても、 $v$ を取り除いても valid な取り方である。
    • このとき、 $S$ 中の $w$ 以外の頂点は次数が $|S|-1$ より真に大きいことに注意されたい。

ここで、各頂点の次数により着目すると、どちらの場合でも以下が成立する。

  • valid な取り方がある時、元のグラフ $G$ について、ある閾値 $k$ が存在して次数が $k$ 以上の頂点から誘導されるグラフが完全グラフである。

更に、等号が成立していない場合でもこれは成立し、ある $k$ でこれが成り立ったなら全ての整数 $l \ge k$ についてもこれは成立する( 着目する頂点が部分集合になるので )。

 

これを使って、以下を満たす最小の $k$ を探索する。

  • 次数 $k$ 以上の頂点のみに着目した場合、それらから誘導される部分グラフが完全グラフである。

つまり、 $S$ 側たりうる頂点をなるべく大きく取った場合 ( $V \setminus S$ をなるべく小さく取った場合 ) に対応する。

この場合で invalid であるとは何を意味するか考える。

  • 取り方のおかげで、 $S$ 側は完全グラフであるのでこちら側の条件は無視して良い
  • よって、 $V \setminus S$ に辺が存在することになる

$V \setminus S$ 側の条件は $k$ を増やすにつれ真に厳しくなる(存在しないべき辺が増えていく)ので、これで invalid なら絶対に無理。

逆に、これで valid な $S$ が発見された場合に解の数を数え上げる。

まず $S$ そのものの $1$ 通りに加えて、 $S$ 側について頂点を「ひとつ追加」・「ひとつ入れ替え」・「ひとつ削除」した場合を考える。先ほどの議論よりこれだけ考えれば十分である。

  • $S$ に含まれないかつ $S$ の全てに接続された頂点があれば、その頂点を追加することが許される。
  • $S$ に含まれるかつ $S$ 以外に辺が全く伸びていない頂点があれば、その頂点を削除することが許される。

実は、ひとつ入れ替えについては考えなくてよい。

証明:

  • $S$ の取り方より、 ( $S$ に含まれる頂点の次数 ) $>$ ( $V \setminus S$ に含まれる頂点の次数 ) が言える。等号が含まれないことに注意。
  • この状況下で頂点を入れ替えてしまうと、 $S$ 側の頂点 $u$ と $V \setminus S$ に含まれる頂点 $v$ であって ( $u$ の次数 ) $<$ ( $v$ の次数 ) なるものが存在してしまうため、不正である。

この一連の流れを実装することで、この問題に正解できる。

 

https://ideone.com/Xb0HFN

次数をうまく使ったトリックのような問題。想定解を読解してこの証明まで辿り着いたが、こんなのどうやったら自力で思いつけるんだ…

Next Permutation (VPCPC 2014 Day4-3)

https://www.acmicpc.net/problem/12825

以下の条件を満たす $(1,2,\dots,N)$ の順列 $P=(P_1,P_2,\dots,P_N)$ を 312-avoid と呼びます。

  • $1 \le i < j < k \le N$ を満たす全ての整数組 $(i,j,k)$ について、 $P_j < P_k < P_i$ となることがない。

312-avoid な順列 $P$ が与えられるので、辞書順で $P$ より大きい 312-avoid な順列のうち辞書順で最小のものを求めよ。

$1 \le N \le 10000$

$P \neq (N,N-1,\dots,1)$

 

問題文に謎の指定があるが、以下の問題が解ければよい。 (初手で $P$ に next_permutation をかけると帰着できる)

順列 $P$ が与えられるので、辞書順で $P$ 以上の 312-avoid な順列のうち辞書順で最小のものを求めよ。

 

312-avoid な順列というのがかなり雲を掴んでいるので、実験してみる。

3 :
0 1 2
0 2 1
1 0 2
1 2 0
2 1 0

4 :
0 1 2 3
0 1 3 2
0 2 1 3
0 2 3 1
0 3 2 1
1 0 2 3
1 0 3 2
1 2 0 3
1 2 3 0
1 3 2 0
2 1 0 3
2 1 3 0
2 3 1 0
3 2 1 0

5 :
0 1 2 3 4
0 1 2 4 3
0 1 3 2 4
0 1 3 4 2
0 1 4 3 2
0 2 1 3 4
0 2 1 4 3
0 2 3 1 4
0 2 3 4 1
0 2 4 3 1
0 3 2 1 4
0 3 2 4 1
0 3 4 2 1
0 4 3 2 1
1 0 2 3 4
1 0 2 4 3
1 0 3 2 4
1 0 3 4 2
1 0 4 3 2
1 2 0 3 4
1 2 0 4 3
1 2 3 0 4
1 2 3 4 0
1 2 4 3 0
1 3 2 0 4
1 3 2 4 0
1 3 4 2 0
1 4 3 2 0
2 1 0 3 4
2 1 0 4 3
2 1 3 0 4
2 1 3 4 0
2 1 4 3 0
2 3 1 0 4
2 3 1 4 0
2 3 4 1 0
2 4 3 1 0
3 2 1 0 4
3 2 1 4 0
3 2 4 1 0
3 4 2 1 0
4 3 2 1 0

 

観察した結果、以下が言える。

  • 312-avoid な順列全体の集合と、以下の手順で生成できる順列全体の集合とは一致する。
  • まず、 $1$ 以上 $N$ 以下の整数 $x$ を好きに選んで $P=(x)$ から始める。
  • その後、以下の手順を $i=1,2,\dots,N-1$ について繰り返す。
    • $P$ の末尾に、以下の条件を満たす要素を付け加える。
      • 集合 $S$ を、現在の $P$ に含まれていない $1$ 以上 $N$ 以下の整数の集合とする。
      • $l$ を、 $S$ 中の $P_i$ 未満の要素のうち最大のものとする。そのようなものがなければ $l=-1$ とする。
      • このとき、 $x$ が $x \in S$ かつ $x \ge l$ を満たす、またその時に限って付け加えることができる。

ざっくり言うと、値が増える時は好き勝手にして良く、値が減る時はそのような要素のうち最大のものしか付け加えられない。

証明は次の通り。

必要性:

もし $l$ 未満の要素 $m $ を付加したとすると、それ以降に $l$ を付加することになる。このとき、 $(P_i,m,l)$ という部分列が存在してこれが 312 型になってしまうので不適。

 

十分性:

ある 312 型の部分列 $(x,y,z)$ が存在すると仮定する。

$x$ を付加した後に $y,z$ ( $y<z$ ) をこの順に付加することになるが、 $y,z < x$ である。

「下る時は下れる最大の要素しか付加できない」という縛りがあるので、必ず $y$ の前に $z$ が付加されることになるので、矛盾。よって、そのような部分列は存在しない。

 

よって、生成方法を暴き出すことができた。

あとは、(帰着した問題での)順列 $P$ を先頭から舐めていき、

  • $P$ の接頭辞が上記の生成法で生成できる限り、それを採用する。
    • 接頭辞が生成できるなら、そのような接頭辞から常に 312-avoid な順列が一つ以上生成できることに注意
  • $P$ の接頭辞が上記の生成法で生成できなくなれば(下がりすぎている状態)、そこからは貪欲に付加できる最小の要素を付加することを繰り返せばよい。

https://ideone.com/DJzJMR

 

必要十分条件を「生成法」のように表現してそこから解いていくという流れは典型だが、その流れが綺麗に適用できたのでメモ。

 

하이퍼 가짜 초콜릿 - Hyper fake chocolate (Baekjoon-28263)

https://www.acmicpc.net/problem/28263

以下の条件を全て満たす長さ $11$ の整数列 $p_1,p_2,\dots,p_{11}$ を一組見つけよ。

  • $p_i$ は $10^7$ 以上 $10^8$ 未満の素数
  • $p_i < p_{i+1}$ ( $1 \le i \le 10$ )
  • $N = p_1 \times p_2 \times \dots \times p_{11}$ はカーマイケル数である

こんな簡潔な output only が Ruby V らしい。戦ってみよう。

 

前提知識: コルセルトの判定法

$n$ がカーマイケル数であることは、以下と同値である。

  • $n$ の素因数 $p_i$ は全て奇数である。
  • $n$ は square-free (重複した素因数を含まない) である。
  • $n$ の全ての素因数 $p_i$ に対して、 $(n-1) \mod (p_i-1) = 0$ である。

Korselt's Theorem - ProofWiki

 

問題の制約より上 $2$ つの条件は自明に満たされるので、 $3$ つ目の条件を吟味する。

この条件は以下のように言い換えられる。

  • $(n-1) \mod \rm{lcm}$$(p_1-1,p_2-1,\dots) = 0$

ここで、この条件を「満たしやすい」ようにするには $\rm{lcm}$ を小さくすればよいという直感が働く。

ここで、 $p_i = k_i \times l + 1$ と生成することを考える。このとき、 $n-1$ は $l$ の倍数となる ( $n = \prod{p_i} = ml + 1$ ( $m $ は整数 ) ) ので言い換えた後の $\rm{mod}$ について $k_i$ の部分しか考えなくて良いことがわかる。

さらに、 $k_i$ を高度合成数 $X$ の約数の部分集合とすることを考える。このとき、十分多くの個数の $10^7 \le p_i < 10^8$ なる素数が生成できれば、 $\rm{mod}$ 部分が $Xl$ となるので、生成された素数の中から $11$ 個選んで条件を満たす確率が $1/X$ 程度だという大胆予想が立つ(仮に $1/X$ でなくともこれを大きく下回っていなければよい + 一組見つけよという問題なのでいったん信じる)。

この「十分多くの個数 $k$」であるが、 $C(k,11)$ がそこそこ大きければよく、例えば $k \ge 45$ 程度あれば $11$ 個の素数の選び方は $10^{10}$ 通り確保できる。

 

以上の流れは、次の二段階の探索を用いて実装できる。

  • まず、素数を生成する式 $p_i = k_i \times l + 1$ の $l$ の部分を探索する。ある高度合成数 $X$ を固定した上で $l$ をいろいろ試して、より多くの $X$ の約数 $k_i$ について $10^7$ 以上 $10^8$ 未満の素数を生成するものを見つける。
    • この結果、ある素数の集合 $P$ が得られる。
  • 次に、サイズ $11$ の $P$ の部分集合を色々と探索する(乱択等でよい)。ここで得た集合に対してコルセルトの判定法を適用し、カーマイケル数を発見次第それを出力する。

試行錯誤の結果得たのが次のコード。確かにカーマイケル数を発見できている。

https://ideone.com/54qW75

高度合成数や $l$ のとりかたがこれと違っても、マシンパワーでぶん回すなどすれば見つかると思います

 

お気持ちに素直に従えば解が見つかる構築問題、大好きっす…

Fortnite (CFR959-H)

Problem - H - Codeforces

(だいぶ換言した) 問題概要

関数 $f(A)$ は数列 $A=(A_0,A_1,\dots,A_{|A|-1})$ を引数に取り、未知のパラメータ $p,m $ を用いて以下の通りに定義される。

$\displaystyle f(A) = \sum^{|A|-1}_{k=0} A_k \times p^k \mod m $

以下の条件を全て満たす数列 $B$ を用いて、関数 $f(B)$ の値を $3$ 度まで尋ねることができる。

  • 数列 $B$ は長さ $1$ 以上 $50$ 以下
  • 数列 $B$ の全ての要素は $1$ 以上 $26$ 以下の整数

$p,m $ を特定せよ。

但し、 $p$ は $27$ 以上 $50$ 以下、 $m $ は $p+2$ 以上 $2 \times 10^9$ 以下の整数である。

↑ 後々分かることだが、これらの制約はかなり重要。

 

本題に入る前に、追加で $\displaystyle g(A) = \sum^{|A|-1}_{k=0} A_k \times p^k$ ( つまり、 $\rm{mod}$ を取る前の $f(A)$ ) と定義しておく。

 

気付きにくいが指摘されると自明な処理として、まず $f([1,1])$ を尋ねることを考える。

このとき $g([1,1]) = p+1$ であり、 $m $ が $p+2$ 以上であることから $g([1,1]) = f([1,1])$ が成り立ち $p$ を特定できる。

 

ここから質問を $2$ 回使って $m $ の特定に入る。天下り的だが、 $g([26,26,\dots,26])$ が $m $ に対して十分大きくなるように尋ねる。

$p \le 50$ であることから、 $g$ が $10^{13} \sim 10^{16}$ 程度となる ( long long で扱うにはちょうどよい ) ような長さの列を見つけることができる。

ここでの $g([26,26,\dots,26])=big$ 、 $f([26,26,\dots,26]) = d$ とする。

 

とりあえず、 $g(B)=big-(d+1)$ なる列を探したくなる。このような $B$ に対しては、 $m = f(B)+1$ である。

もし $B$ としてどんな列でも使ってよいなら $[x,26,26,\dots,26]$ の $x$ を $26-d-1$ とすればよいが、全ての要素が $1$ 以上 $26$ 以下という縛りがあって困ってしまう。

増してや、 $g([x,26,26,\dots,26])=g(B)$ となる合法的な $B$ が存在しないかもしれない ( 例えば $p=50,x=0$ だと詰む )。

 

$g$ に対する要求をもう少し緩めたい。ここで、次のことが言える。

$big-2d \le g(B) \le big-(d+1)$ なる列 $B$ について、 $m=f(B)+(big-d)-g(B)$ が成り立つ。

直感的には、 $f([26,26,\dots,26])$ が $d$ だった ( $\mod m $ 上で $d$ だけ余裕がある ) ので、 $big-d$ からもう一度 $d$ を引いても 「 $big-d$ から余計に引いた数 + 余り $=m $ 」という性質を崩すことなく安全に引ける ( $big-d \rightarrow big-d-1$ 以外で $\mod m = 0$ となる数を跨ぎ超えることがない ) という感じ。

本当にひとことで理解を済ませるなら、「 $m $ で割った商を変えずに $d$ 引けるのだから、 $2d$ 引いても引きすぎにはならない」とでも言ったものか。

 

では、 $big-2d \le g(B) \le big-(d+1)$ なる列 $B$ はどう見つければよいのか? そもそも存在するのか?

 

$d=0$ である場合は不等式が偽だが、そう難しくない。要するに $f([26,26,\dots,26])=0$ なので、 $f([25,26,\dots,26])=m- 1 $ となりこれを尋ねてやればよい。

そして、 $d \ge 1$ である場合は $big-2d \le g(B) \le big-(d+1)$ なる列 $B$ が必ず存在する。証明の概略は次の通り。

  • $0$ 要素目を $26-k_0$ とすることで $-k_0$ ( $0 \le k_0 \le 25$ ) が表現できる
  • $1$ 要素目を $26-k_1$ とすることで $-p \times k_1$ ( $0 \le k_1 \le 25$ ) が表現できる
  • $2$ 要素目を $26-k_2$ とすることで $-p^2 \times k_2$ ( $0 \le k_2 \le 25$ ) が表現できる
  • $\vdots$

ここで $p \le 50$ が活きる。いったん $p=50$ として考えてみると

  • $-1$ は $k=[1,0,0,\dots]$ として表現できる
  • $-2$ は $k=[2,0,0,\dots]$ として表現できる
  • $\vdots$
  • $-25$ は $k=[25,0,0,\dots]$ として表現できる
  • $-50$ は $k=[0,1,0,\dots]$ として表現できる
  • $\vdots$
  • $-1275$ は $k=[25,25,0,\dots]$ として表現できる
  • $-2500$ は $k=[0,0,1,\dots]$ として表現できる
  • $\vdots$

$p \le 50$ であるおかげで、表現できる数で隣り合ったもの $a,b$ について、 $2a \ge b$ が成り立っている ( $2$ 倍を超える差がつくことがない )。

これで存在性は示せた。

あとは $k$ の構築だが、これはかなり何をしてもできる ( $-(d+1)$ 以下で最大の表現を二分探索、後ろから貪欲 etc...  自分の実装は「後ろから貪欲」の方針 )。

 

Submission #271311959 - Codeforces

 

制約がちょっとずるい気もするが、常に誤差 $2$ 倍以内に収めることができる ( $d+1$ 以上 $2d$ 以下を引き去ることができる ) という点を上手く利用する点がかなり面白く感じた。

公式解説等にも同じことが書いてあるが、お気持ちが分かりづらかった(ここに書いたような理解をするとすんなり理解できた)のでメモ。

これ自力で思いつくにはどうすればいいんだろう 多分天才に生まれ直すのが一番早いと思います

$2$ 回目に $[26,26,\dots,26]$ を尋ねる発想は、「いずれ $f([26,26,\dots,26])+1$ くらいの数を引き去るという操作をしたいが、そのような操作を数列上で行えるようにする」というところから持ってこれるかもしれない。

Tandem Repeats(SER2013-G)

Tandem Repeats

長さ $L$ ( $L \le 10^5$ ) の A,G,T,C からなる文字列 $S$ が与えられる。

この文字列のうち連続する $2k$ 文字の連続部分列であって、同じ長さ $k$ の文字列が $2$ 度繰り返されているものの数を数えよ。

(文字種の制限は使わないので、任意の英大小文字からなる文字列だとしても別に良い)

 

繰り返しのひとつあたりの長さ $k$ を固定して、 $O(L/k)$ 程度で解くことを考える。こうすると調和級数の $\log$ 1つを増やせば元の問題を解ける。

 

結論から言ってしまうと、次の手順で解ける。

  • 文字列の $1$ 回目と $2$ 回目との仕切りの位置を固定し、これを文字列の左端から右端へと動かすことを考える。 CATTCGATTCGAT は、仕切りが $6$ 文字目の直後に入っているイメージ。
  • もし、今注目している場所の両側で文字列が一致しているなら、その部分はまともと認定して仕切りを $k$ 文字右に進める。
  • そうでないなら、不一致となる文字の組のうち最も右にあるものを検出し、そのうち片側を追い出すように仕切りを右に進める。(両側が残っている限りふたつの文字列は揃わないことに注意)

図中青の仕切りを緑の位置に動かすような感じ。

文字列が不一致となる位置の検出は、ロリハで $\log$ を1つ増やせばできる。

 

これが $O(L/k)$ 回で済む証明は次の通り。

  • 文字列が一致しているパターンは、仕切りが一度に $k$ 文字右に進むので明らか。
  • 文字列が一致しないパターンで例えば右から $t$ 文字は一致していたとする。このとき仕切りは $k-t$ 文字右に進む。その次の仕切りの操作を考えた時、その時点での文字列のうち左から $t$ 文字は揃っていることが保証されるため、少なくとも仕切りは $t$ 個以上右に進む。なので、結果として $2$ 手で $k$ 文字以上仕切りが右に進む。

より詳細には、文字列が一致しているパターンの直後は連続して文字列が一致している部分が存在しているパターンがある (AGCAGCAGCT のような場合) ので、その数を数えなければならない。文字列が一致しているパターンの連続の場合は定数時間、一致しているパターンの直後に一致していないパターンを引いた場合は最も左の不一致の検出の $\log$ 1つでできる。これ以上の詳細は実装参照。

結果、全体で $\log$ 2つでこの問題に正解できる。

https://ideone.com/VXeNUf

「一見厳しそうだが実は間に合う」という、計算量解析が美しい問題。

 

想定解は $\log$ 1つっぽい見た目をしているが、読解できなかった…

AHC034 参加記

画像

誤った成功体験

 

A - Leveling with a Dump Truck

初手 : 「足りない」「余ってる」どちらにせよ、全マスを 2 回巡れば全マス 0 にはできるので、これを実装。マスの高さは過不足を調整できるだけ調整。

S字を描くように巡って 260 、渦を描くように巡って 384 。

渦を巻いたのは道中の重さの偏りを軽減するため。

しかし、この時点で 500 近い得点を出している方がいたのでいったん方針を棄却。

S字を描く 260

 

渦を描く 384

 

1 手目を終えて、おおよそ 1 時間くらい。

 

2手目 : 「最初に列で総和を揃え、その後行を合わせる」

列で総和を揃えれば低コストで行をなんとかできると予想。

最も左の列で総和を揃えて 519。

この時、改良として「2列ずつ見て、奇数列目で積んで偶数列目で積み下ろせばコストが減らせるのでは」と予想し取り入れるも 527 。

この時点で 700 台がいたのでこの方針も一旦棄却。

左端の列で行の総和を調整する方針 519

奇数列目で積んで偶数列目で積み下ろして調整する方針 527

 

2手目を終えて、おおよそ 1 時間 40 分くらい。

 

ここで、一度得点が 800 くらいになるとはどのようなことか考えてみる。

自分のスコアから逆算して、「おおよそコスト 13 万以内に抑えれば 800 」ということが分かる。

重大な事実として、全てのマスを巡るのに 4 万コストかかる。ここで、次の2択を迫られる。

  • 全てのマスをおおよそ2回巡って残りコスト 5 万
  • 全てのマスをおおよそ3回巡って残りコスト 1 万

そもそも $|h_i|$ が 25 くらいなのに後者はさすがにダメだろ… という直感で後者を棄却、前者の方向で進めていく。

残りコスト 5 万として、一歩当たりの積載量は 60 くらい。最初はこれをヒューリスティックに達成しようとしたが失敗して 30 分から 1 時間ほどロス。この時 LayCurse さんが 810 くらいを出していてまだ上があることを把握。この時点で 2 時間だったのでここから先心が折れないよう順位表情報をシャットアウト。

流石に積載量 60 をヒューリスティックするのは無理だと確信し、ひとまずコストの自明な下界を見積もろうとする。このとき、最初はマンハッタン距離でMCFしようとしたが、よくよく考えてみればマスの巡り方をそのままフローの辺に見立ててよいことに気づく。

図は、マスを綺麗に 2 巡した場合のダンプの動き方。

意識としては、砂を図中の矢印向きのコンベアに従って動かす感覚。適当に 2 マスをとって最短路を見てもらうとわかるが、 2 巡(本来欲しい 4 方位の半分くらいしか辺が無い)しかしてないのにほぼほぼ遠回りすることはないことが分かる。

画像

このままフローを、流します(力技) 赤が 1 巡目、青が 2 巡目

 

土壌はいくら削りとってもいいようなものなので、一回「どこの砂をどこへ運ぶ」みたいなことは忘れて、とにかく各辺の時点でMCFのフロー分だけ砂を運べばいいことになる。この時点で MCF に対応する輸送が復元できることがわかり、 MCF の重みだけ見ると (2巡ぶんのコスト 80000) + 39000 とかが出てきた ( 最終コスト 119000 ) ので、これが 2 時間時点でのトップクラスの方針だと確信、実装して 777。

この時点でも実行時間は数msだったので、この解を結構な回数実行できることも分かる。

また、 ウォークを取る(=MCF を流す)際に、なるべく「2 巡で使っていく辺が直交する」ように取ることを意識するようにする。こうすることで、無駄な辺を増やさずに効率的に輸送できる辺群が取れるという意識を念頭に?潜在意識に?置いて考察することに。

この時点で3時間食ってしまった。ここまではもたついてダメだったと反省。

しかし、これが神打開の始まりだった。ここからは本当に冴えていた。

 

全体を綺麗に2巡してMCF 777

 

ここで、先ほどのビジュアライザを見ると縦縞がけっこう見えることに気づく。なので、「1巡目か2巡目は綺麗に舐めなくてもいいのでは?」と気づく。

そこで、「1巡目か2巡目は1列飛ばしに舐める」という方針を取り入れる。これで 790 を受け取った。但しこの提出は本番提出がバグっていてスコアが不正確なので、方針だけ採用して正しく実装しなおした画像を載せる。

 

1列飛ばし 790 (正しく実装すれば874)

 

ここからは2巡目の歩数を削っていく。全体を巡るウォークを何通りか作っておき、ウォークのうち一番最後の歩みを消して求解を繰り返す。これで 899 。

 

1列飛ばしかつウォークの最後を削る 899

 

その後、「飛ばす段数は別に1段に限らなくてもいいので、2, 2.5, 3, 4段飛ばしというようにいくつかパターンを作ってから、時間が許す限り各パターンの後ろを削り続けることを試す」「1回目に k 段飛ばし・2回目に k 段飛ばし どちらも実装しているが、前者は全くといっていいほど採用されていないので切り捨てて後者のパターンに限定する」を追加して 918 に着地。

 

最終提出 918

 

さて、順位表を見てみると… まさかの 2 位。嘘だろ…

 

Submission #54643078 - Toyota Programming Contest 2024#6（AtCoder Heuristic Contest 034）

 

次の一手が取れたとするなら、ウォークの取り方で焼いたりするのだろう。もっとも自分にそれはもう 4 時間あっても厳しいだろう… (絶望)

 

優勝した yosupo さんは直交したウォークから始めて山を登っているらしい。 4 時間でそこまで辿り着くの強すぎる！

 

勝因としては、序盤から中盤にかけて方針を 2 回棄却できたことだろう。そう難しくない実装で 2 時間時点でのトップクラスが出ないならその方針は捨てた方がいいのだろうか…

New Year and Castle Construction (CF Hello2020-E)

Problem - E - Codeforces

$xy$ 平面上の $N$ 点が与えられ、点 $i$ は $(x_i,y_i)$ にある。このとき、異なる $3$ 点は同一線上にない。

以下の通り $f(k)$ を定義する。

まず、点 $k$ を除いた $N-1$ 点の中から $4$ 点 $A,B,C,D$ を選択する。

このとき、 $A,B,C,D$ を結んで (凸でなくともよいが、非退化な) 多角形を構成することを考えるとき、点 $k$ を内部に含むことができるという。

$f(k)$ を、以上が成り立つ $4$ 点の組 $A,B,C,D$ (順序の違いは区別しない) の個数とする。

$\sum^{N}_{k=1} f(k)$ を求めよ。

制約

・$5 \le N \le 2500$

・$|x_i|, |y_i| \le 10^9$

まず、 包囲(ttpc2015-H) - physics0523's 精進ログ でも述べた通り、平面上のある点を内部に包含する冗長でない図形は「三角形」「包含したい点を対角線上に含む四角形」の $2$ 通りだけです。しかし、この問題の制約上 $3$ 点が同一直線上にないので、考えるべきは前者だけです。

次の場合分けを考えます。

  • 選んだ $4$ 点の凸包が四角形である
  • 選んだ $4$ 点の凸包が三角形である

実は、このどちらであろうと、以下の事実が成立します。

  • もしこの $4$ 点が点 $k$ を包含するなら、選んだ $4$ 点の中から $3$ 点を選択した時に点 $k$ を包含する三角形が丁度 $2$ つ存在する。

以下のように図証します。

 

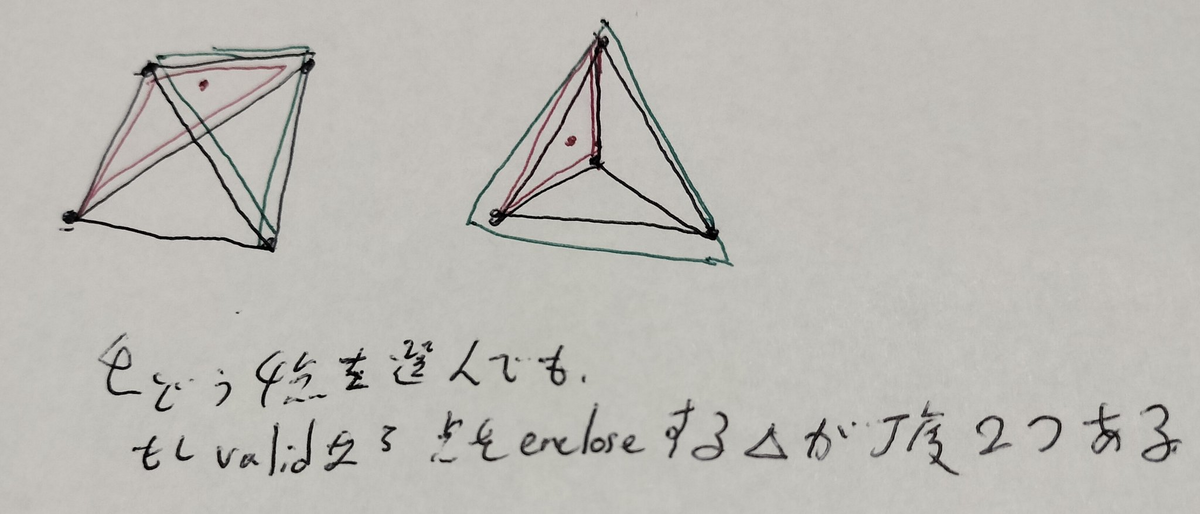
すると、主客転倒の考え方を使うと求めるべき値は以下のように言い換えられます。

  • 全ての点 $k$ について、点 $k$ を包含する三角形の個数を数え上げ、それを $T$ とする。答えは全ての点 $k$ について $T \times (N-4)$ を足し合わせ、それを $2$ で割ったものとなる。

要するに、三角形と内包される点を選択したら、あと $1$ 点は自由に取れ、このもとでありうる全ての $4$ 点組を $2$ 度カウントするということです。

 

この時点で、求めるべきはある点を包含する三角形の個数を数える問題になりました。これは、偏角ソートを使うと解くことができます。具体的には次の通りです。

  • 点 $k$ を包含しない三角形の個数を数える。この時、点 $k$ を中心に据えると三角形の点が反時計回りに $A,B,C$ と並ぶとする。すると、 $\angle AkC, \angle BkA, \angle C k B$ のうち丁度 $1$ つが $180^{\circ}$ 未満となる。 (これらの複数が $180^{\circ}$ 未満 となることはありえないことに注意されたい) 
    • 逆に、これが成り立たない時は三角形が必ず点 $k$ を包含する。
  • この事実を使うと、尺取り法の要領で数え上げをすることができる。

以上より、この問題を時間計算量 $O(N^2 \log N)$ で解くことができました。

Submission #265114188 - Codeforces

 

どう点 $k$ を囲む $4$ 点を選んでも、その中で点 $k$ を囲む $3$ 点が必ず丁度 $2$ 組存在するという巧みな不変量を利用した美しい問題。