Water Bottle(ABC144-D)
ABC144-Dのおきもちをざっくり1枚にまとめました#AtCoder pic.twitter.com/MFZcLIupaf
— 物理好き@新感覚競プロ魔法少女物語「魔法少女ぶつりょな∇」11月9日放送開始! (@butsurizuki) October 27, 2019
Fork in the Road(ABC144-F)
想定解より良いオーダーだったので書きます
まず、元のグラフについて、そのノードを通る確率を前から計算していきます。
ノード番号の若いほうから以下の図のような遷移をすると可能です。
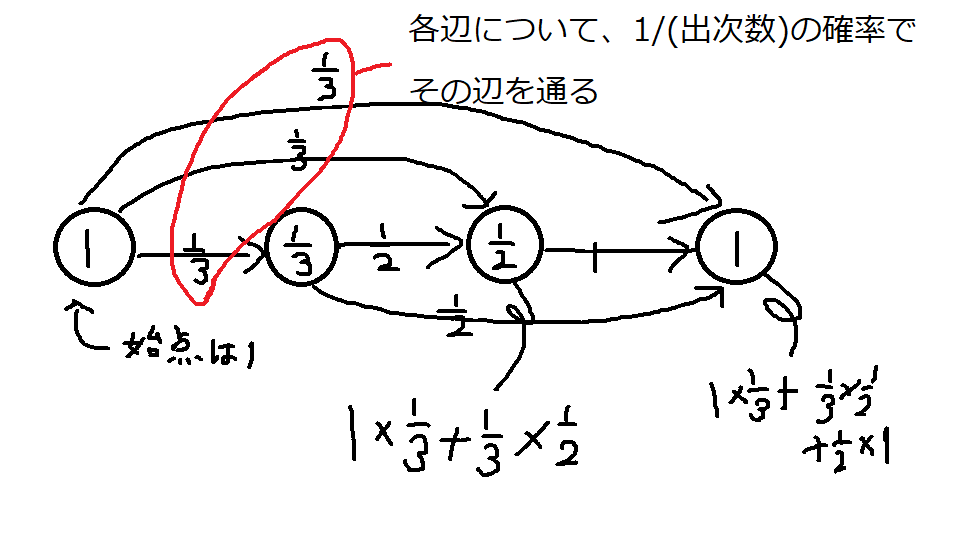
今度は、「そのノードからあと何ノードたどればゴールできるかの期待値」も計算してみましょう。これは右側(頂点番号)の大きい方から探索していきます。
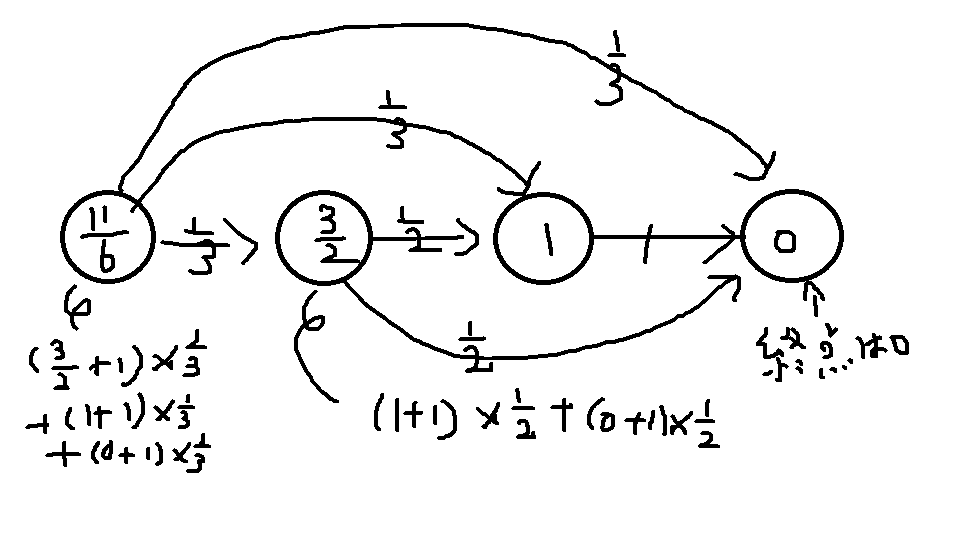
最後に、それぞれの辺に着目して、その辺を消すと「そのノードからゴールまでの手数の期待値」がどのくらい改善されるのかにそのノードに入る確率を掛けたものが全体の改良幅となるので、それの最小をとったものが解です。
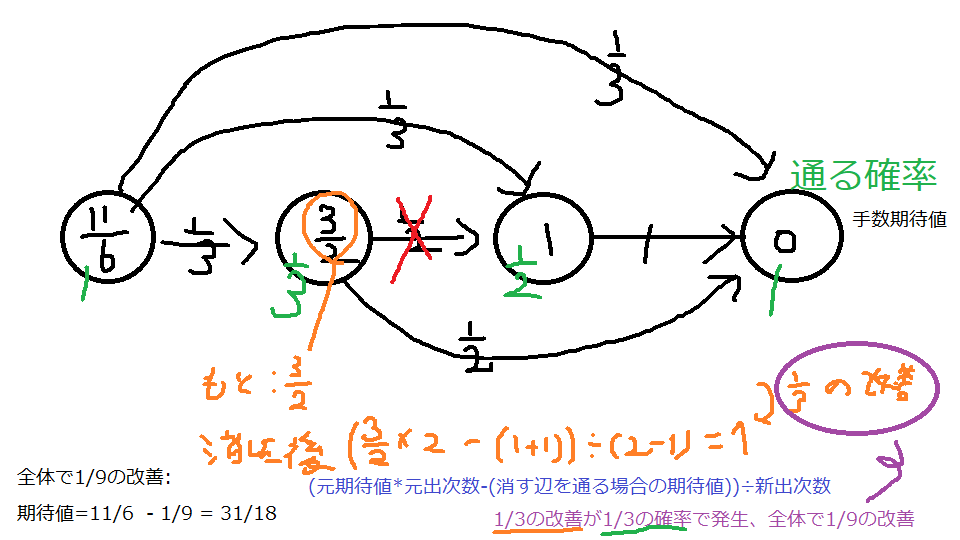
計算量ですが、どのステップでも各辺に対して1度の操作を行うことになるので\(O(M)\)です。
【独白】物理好きが個人的に語る、butsurizuki Beginner Contestの作り方、競プロでの作問の仕方
最近ブログをほとんど更新できていないので、折角なので僕が作問するときに意識していることを書いてみます。
実は、僕はABCに近い難易度と体裁のセットを、1人で(基本的に)1日で作り上げてそれをHackerRankのコンテスト開催機能を活用して有志コンとして実施するという伝統をしています。
実際、過去に2度実施されています。
BBC001 (2019/03/10 21:00 ~ 23:00 42人参加)
BBC002 (2019/10/12 21:00 ~ 23:00 91人参加)
このコンテスト、準備期間が1日かつ1人で準備しているためTesterもいないというはたからみるとかなり狂った感じのコンテストに見えます。
しかし、実際のところ、自分が今まで携わったコンテストの中ではclar(clarifications,質問)もあまり飛ばないほうで、重篤な事故もまだ起きていません(本音を言うと正直事故はまだ起きていないだけ…という気もしますが)。しかも、参加者も有志コンの中では相当獲得できていると思います。
コンテストを1日かつ1人で準備してもある程度高い精度を出すために個人的に意識していることをまとめます(すでに界隈でよく言われていることも多く含まれますが)。有志コンやってみたいな~と思っている方は参考にしてください。
作問編
ここでは、主に問題原案を作る段階で意識していることを示します。
低難度は、問題から配点よりも配点から問題を作る
正直これは意識していることというより意見に近いですが、低難度は「問題に配点を与える」ではなく、「配点から問題を作る」方が有効だと思っています。例えば、100点ならmax()や足し算引き算などで1発で答えが出るとか、200なら全探索が利くとか…といったことです。正直300以上となるとけっこう配点が揺れるので、この方法は実際は100とか200とかが欲しい…と思ったときに結構有効です。
問題破綻を防ぐために常に解説を意識する
問題が破綻している…といったことを防ぐために、常に「解説を執筆する」ということを意識しましょう。解説には解法の証明、最低限正当性を示す文章を書くことになるので、それが書けるかな~といったことを意識すると、破綻する確率は下がります。
「貼るだけ」は回避する
ある程度難易度の高い問題を作るときに、あまり語られていなさそうなフレッシュな話題を持ち込みたい…と思ったときに、その話題はなるべく「変形または考察をすると使える…」といった形にしましょう。最悪、ネットに転がっているライブラリや実装例を貼るだけで通る…というのは避けましょう。
その解法が聞かれている問題の点数の相場を把握する
「○○点だから△△法はない」という考え方はよくないとは言われますが、点数がある程度難易度の絶対評価になっている環境である以上、アルゴリズムには相場の点数が付いてしまいます。ある程度の問題数を解いてみると、○○法はだいたい何点で訊かれることが多い~といったことが把握できます。これは配点の決定に大いに有用です。
嘘解法、非想定解法を想定する
これはかなり重要です。自分が想定していない解法をいくつか考えましょう。例えば、想定解法から途中で解法を分岐させるなどすると有用です。そのうえで、その解法を落としたいか落としたくないか決めましょう。例えば、気付けた嘘解法は明らかに落とすべきです。嘘貪欲や嘘乱択が効いてしまいそうな場合、そのアルゴリズムのあらましを想定したうえで反例を考え、反例となるケースを確実にテストに入れましょう。反例はいろんなパラメータが極端なケースで起こりやすいです。もし反例が思いつけない場合は、その解法が正しい別解となりうることも想定しましょう。次に、オーダーの悪い正当な解法です。これを通すか通さないかは正直作問者のさじ加減です。たとえば、O(N)が想定でO(N√N)が見つかった場合、もしN√Nを認めたいならN≦10^5程度に設定し、落としたいならN≧10^6に設定する、または実行時間制限を厳しくするなどしましょう。もし落としたい解法を本当に落とせているか不安なら、実際に実装して実測しましょう。
作文編
ここでは、主に問題文を作る段階で意識していることを示します。
クソリプを想定する
突然ですが、Twitterには「クソリプ」という用語があります。「クソリプ」とは「クソみたいなリプライ」の略で、ツイートの筆者の上げ足をとるような返信のことです。これと同じように、コンテスタントは作問者の上げ足を取りに来ると思うとよいです。なので、自分で自分の文章を読んであげ足を取ろうとしてみて、実際に取れたものから潰していく…という作業を繰り返すと問題文の精度は上がります。
しつこいくらいに厳密に書く
問題文の表現として、「個数A_i」ならA_iは0以上の整数だと読み取れますが、「価値A_i」だとA_iは正のみなのか負も含まれるのか、整数なのか実数なのか分かりません。コンテスタントがサンプルを見て察してくれればありがたいのですが、たまに察してくれない場合もあります。なので、制約欄に「入力は全て整数である。」というように明記しておくと親切かつclarも避けられます。
さらに、「1≦A_i≦10^9」のような制約を入れたい場合は、iに関する制約(1≦i≦Nなど)を忘れずに入れておくようにしましょう。
伝わりにくい場合はサンプルで補足する
(厳密に問題文を書いたがゆえに?そうでなくとも日本語に自信がない場合など、)読解難易度が上がってしまっている場合、サンプルにおいて問題文が指示しているような操作を実際に行ってみるとどうなるか…というような流れをある程度丁寧に説明していきましょう。わかりやすいサンプルは問題文の読解を助けます。
特殊な入力は丁寧に説明する
入力が特殊な場合は丁寧に説明しましょう。
例えば、迷路のようなものを文字列で与える問題だと、「#は壁で、.は空き地である。」というような説明を、問題文か入力欄に入れておきましょう。
更に厄介なのは実数入力で、言語によって仕様が違うなんてことも想定されるので、丁寧に入力の仕方を設定しましょう。例えば、「A_iは小数第2位まで与えられる。」というようにしておけば書式が定まります。この時、3.8などの値は必ず3.80というようにゼロ埋めしましょう。
「バナナはおやつに入りますか~?」
例えば、「ある文字列の部分文字列」という言葉を使いたい場合、その中に空文字列を含めるかどうかは明記するべきです。「自然数」という表現も0を含む流儀と含まない流儀があったりするので「0以上の整数」や「自然数(0は含まない)」、「正整数」といった表現を使うのが確実です。さらには、「最小の操作回数T」という指定などでも、「0は入りますか?それは操作していないと思うんですが…」という観点に備えて0を入れるかどうかは指示しましょう。もう1例挙げると、「周りが海に囲まれた陸地の高さA_1,A_2,...,A_N」という指定があった場合に、「A_1,A_2,...,A_Nが全て0」という、「それは陸地が存在しているのか…?」というようなケースが入るか入らないかもしっかり明記しましょう。もっとも、このような怪しいケースに対して厳密な議論ができる自信がないなら、制約でこのようなケースを除いてやるのも1つの手です。
「数え上げの時に数えたいものが存在しない」という場合にもこの問題は起きて、「0通り」だから出力は0といった暗黙の了解を求めるのは不親切です。「存在しない場合は、0と出力してください」と問題文に明記するか、サンプルに0通りのケースを混ぜましょう。もっとも、「制約で数えたいものが1つは存在する」と縛るのも手です。
インタラクティブでは、必ずflushの指示を入れる
インタラクティブ問題では、ジャッジの仕様上flushを要求されるので、flushの指示をわかりやすく入れましょう(どのインタラクティブを見ても「こんな感じなのか」とある程度みてとれるはずです)。インタラクティブが実装されているどの競プロサイトにもインタラクティブに関するチュートリアル的問題はあると思うので、その問題に誘導をかけておくと吉です。
テストケース編
ここでは、主に問題文を作る段階で意識していることを示します。
サンプルもランダム生成してみる
これは、テストケースの書式がサンプルだけ違っていたりすると、言語によっては入力が正しく行えない…といったことを避けるためです。さらに、テストケースの書式が正しそうかどうかを、ある程度目視で確認することもできます。
サンプルは、解法がばれないギリギリを突く
サンプルから解法がある程度察せるかも…?と思った場合、サンプルは解法がばれないギリギリを突きましょう。例えば、サンプルから解法が察せなさそうな問題はある程度サイズのあるランダムケースを見せたほうが親切です。逆に、サンプルをあまり見せると解法が察されそうな問題では、解法がばれないギリギリを突きましょう。例えば、Yes/No系でNoの例が数個しか存在しない場合はYesの1例とNoの最小例(手で確かめられる程度)の2つだけを見せる、といった場合に解法が察される可能性を下げられます。ちなみにサンプルを考えていくと解法への誘導が若干かかっている、というのも稀にありますが美しさは増して個人的には好きです。
構築の場合、想定解から生成したものはサンプルとしてあまり見せない
構築問題において、想定解から生成したものをサンプルとして見せてしまうと、その構築法から察されて解かれる…といったことが考えられます。なので、サンプルの想定outputでは、できるだけランダムっぽいものをハンドメイドでもしてやりましょう。もっともサンプルから誘導を掛ける場合は話は別ですが。
極端なケースはいろいろ想定する
まず、入力の要素数最大や各要素の最大最小などは容易に想定できます。しかし、実際にこれらがコーナーケースになるよりは、「解の最大値」や「計算量の最大値」、「-1系」などがコーナーケースになる可能性が高いです。
「解の最大値」:問題によってまちまちですが、例えば愚直な操作がO(1)でできるような問題において、実際は操作回数が10^12になるテストケースも考えられるのにテストケースでは10^7程度しか入っていなかった…ということが起これば、なんと愚直解がACしてしまいます。テストケースはinputだけでなく、outputも吟味しましょう。
「計算量の最大値」:入力個数などのパラメータが最大でなくても、入力要素の組によって計算時間が変わって最悪になりうるようなアルゴリズムの場合、それも想定しましょう。
「-1系」:例えば、「○○が存在しない場合、-1を出力せよ」といった問題があります。このような場合、(そもそも-1が存在しない場合はいいのですが)-1となるテストケースは必ずテスト内に含みましょう。逆に、-1でないケースも必ず含みましょう。ランダム生成させただけだと、-1が含まれないまたは-1しか含まれないといった状況に陥る可能性もあります。
実情が制約より緩いのは許されるが、実情が制約より厳しいのは許されない
例えば、「解は10^5を超えない」といった少々特殊な制約を指定したいとします。
このとき、解が99999.99なのは許されますが、100000.01は許されません。当たり前と思われるかもしれませんが、実数が絡む場合は特に、計算された解が誤差を含むなどした場合や解の評価を少し誤った場合、制約ギリギリだと思ったテストケースが制約違反だったということも十分考えられます。このような場合、例えば解が99999.00程度なケースしか含まないようにして、実情が制約より若干緩い…という状況にしてしまうのは1つの手です。
テストケースに役目を割り振る
テストケースを見ると、稀に"small","large","corner"のような文字列を見ることがあります。そのような感じで、「smallを10個、largeを10個、最大を2個、最小を2個、コーナーAを3個、コーナーBを3個」というような感じで、テストケースに分業をさせてやると、より多角的な視点から正確な判定を得ることができます。
グラフ問において、「木」「ウニ」「直線」「完全」グラフだけで安心しない
グラフ問において、「木」「ウニグラフ」「直線グラフ」「完全グラフ」は確かにコーナーケースとして有用な場合が多いです(特に完全グラフは強力なイメージ)。しかし、必ずしもこれがコーナーとして強いとは限りません。これらのグラフを少し変形する(辺をいくつか加える/消す/逆に向ける...)だけでもだいぶ強さが増します。一番いいのは、問題の特性を把握して、思いつく限り最悪のグラフを予測することです。例えば、全探索できてしまわないか、グラフの連結成分はいくつが最悪そうか、この問題特有のコーナーとなりえるグラフの形はないか、といったあたりでしょうか。
愚直解を投げてみる or 愚直解でoutputを作る
愚直解をsubmitしてみるということも大事でしょう。そうすることによって、自分の解法が正当かどうか再度検証するとともに、愚直でTLEするかどうかの判断もできます。愚直解でoutputを作るという方法もあって、愚直から生成したほうが少々時間はかかりますがミスの確率が下がります。
Tester作業系編
ここでは、主にTester作業系をする段階で意識していることを示します。
もう一度1から問題文を読解する
自分で書いた文章が自分で読解できないことは多々あります。不明瞭な点が問題文にあれば、その都度直していきましょう。中には、変数の文字を取り違えているなど、ミスが見つかるほどのものも存在します。
もう一度1から自分の解法を実装する
一度自分でACすることができても不安が残っている場合、もう一度1から自分の解法を実装してみるとよいでしょう。こうすることで、実装ミスでテストケースにエラーが入っているといった可能性を減らすことが出来ます。
assertを使う
assert(条件);で、条件が偽ならプログラムを停止するというようなものがライブラリに存在する場合、それがテストケースが制約を満たすかどうか把握する助けになります。assertが発生したときのジャッジの挙動はまちまちですが基本的にREになる(どのような挙動になるかは調べておく必要があります)ので、例えば制約が1≦N≦100000となっているときにassert(1 <= N && N <= 100000);というような文を入れておくと、これを満たさないケースが含まれた場合にREを起こしてそれの発見が楽になります。
宣伝編
ここでは、主にコンテストの宣伝をする段階で意識していることを示します。
休日の夜を狙って宣伝やコンテストをする
基本的には休日の夜にはインターネットに人が増えます。その時間を狙ってコンテストや宣伝を行えば、かなり人が増えやすいです。もっとも、他のコンテストと被るのはご法度ですが。
別のコンテストの終了直後を狙って宣伝する
別のコンテストが終わった直後は、競プロer各位が解法ツイートをするので多くの人間がTLを眺めています。これを利用して、そのタイミングで宣伝を撃つと多くの人間の目に留まりやすくなります。
時間帯を変えて、何度も宣伝する
基本的には宣伝回数は多いほど吉です。しかも、競プロ界隈は有志コンにも積極的だと思うので、宣伝が多すぎるので悪印象になる…といった可能性は意外と低いです。なので、ガンガン宣伝を撃っていきましょう。時間帯も変えるとさらによいです。Twitterにおいて、朝TLに要る人間と昼TLにいる人間、夜TLにいる人間とでは全く顔ぶれが違います。とにかく、ツイートを見た人間の客層を広げていくことが大事です。
僕が作問やコンテスト設営で意識していることはこのあたりでしょうか(増えれば追記します)。今までWriterに手を出せなかったけどやってみたい…と思っている方にとって少しでも有用なものであれば幸いです。
それでは、よいWriterライフを!!
ABC段位認定のうらばなし
まず、合格基準を3/4に定めた理由としては、問題の当たり外れを緩和するためです。中伝、皆伝を除くどの段位でも3問目と4問目の間の難易度の差は極力抑えており、3問目か4問目のどちらかが解ければ「その難易度層は一定の確率で解ける」と認定できるような選定をしています。
ちなみに、偶数段位の2問目は「X点の最難関」というような問題を置いているので、そこでハマらないように注意してください。
問題の難易度についてはおおよそ以下の通りです。(次回以降の段位認定では、700点以上は600詐称級の問題を持ってくることになると思います。)
同じX点でも、原則として上の段位にある方の問題が難しいです。
例えば初段1問目のA - 積雪深差と二段2問目のA - Happy Birthday!とは同じ100点でも大きく難易度が異なります。
初段 100-100-100-100
二段 100-100-200-200
三段 200-200-200-200
四段 200-200-300-300
五段 300-300-300-300
六段 300-300-400-400
七段 400-400-400-400
八段 400-400-500-500
九段 500-500-500-500
十段 500-500-600-600
中伝 600-600-700-700
皆伝 600-700-700-800
各段位のおおよその認定基準は以下の通りです。
初段:100点が3/4以上の確率で解ける
二段:200点が1/3以上の確率で解ける
三段:200点が3/4以上の確率で解ける
四段:300点が1/3以上の確率で解ける
五段:300点が3/4以上の確率で解ける
六段:400点が1/3以上の確率で解ける
七段:400点が3/4以上の確率で解ける
八段:500点が1/3以上の確率で解ける
九段:500点が3/4以上の確率で解ける
十段:600点が1/3以上の確率で解ける
ここまで受かれば新ABC卒業と言っても大丈夫だと思います。
これ以上は新ABC卒業生でも合格は困難です。
中伝:700点以上でも十分戦っていける地力
皆伝:700点は高確率で解け、800点以上でも十分戦っていける地力
AtCoder Beginner Contest 非公式段位認定 2019夏
AtCoder Beginner Contest (001~132) の過去問を利用した段位認定コースです。
僕のABC完全全完記念に作ってみました。
2時間で4問を解いてください。その結果により、実力を判定します。
| 正解問題数 | 判定結果 |
|---|---|
| 0,1問正解 | 合格にはまだまだ精進が必要です。 |
| 2問正解 | あと少しです、ひとつ下の段位に余裕をもって合格可能です。 |
| 3問正解 | 合格です!おめでとうございます! |
| 4問正解(全完) | 金合格です!!ひとつ上の段位にも充分挑める地力です!! |
- 初段(Rating:200)
- 二段(Rating:400)
- 三段(Rating:600)
- 四段(Rating:800)
- 五段(Rating:1000)
- 六段(Rating:1200)
- 七段(Rating:1400)
- 八段(Rating:1600)
- 九段(Rating:1800)
- 十段(Rating:2000)
- 中伝(Rating:2000+)
- 皆伝(Rating:????)
初段(Rating:200)
合格でおおよそレート200相当です。
二段(Rating:400)
合格でおおよそレート400相当です。
三段(Rating:600)
合格でおおよそレート600相当です。
四段(Rating:800)
合格でおおよそレート800相当です。
五段(Rating:1000)
合格でおおよそレート1000相当です。
六段(Rating:1200)
合格でおおよそレート1200相当です。
七段(Rating:1400)
合格でおおよそレート1400相当です。
八段(Rating:1600)
合格でおおよそレート1600相当です。
九段(Rating:1800)
合格でおおよそレート1800相当です。
十段(Rating:2000)
合格でおおよそレート2000相当です。
中伝(Rating:2000+)
合格でおおよそレート2000以上相当です。
皆伝(Rating:????)
歴代ABCの中でも最上級の難易度の4問です。
ABCといえども合格、金合格には相当な地力が要求されるでしょう。
好評なら、次回のコースは新ABCの問題が増えてきた秋頃に組んでみようと思います(全段位合わせて48問必要なのでABCを3か月分くらい食ってしまいます…)
歩くサンタクロース(JOI2011本選 問4)
まず、状況を整理すると、ある点Pを1点定めて、そこから「指定されたN点のマンハッタン距離の2倍からPから最遠の点までのマンハッタン距離を引いたもの」を最小化する問題です。(点Pは明らかに点が存在する長方領域の中です)
結論から言うと、点集合の各座標をソートしてそれぞれの座標で中央値を取ったもの(ただし、Nが偶数の時は小さいほうからN/2番目の座標か(N/2)+1番目の座標のどちらかを取る)の最大4点のうちのどれかになるので、これを(幾何的に)証明します。
(以降、マンハッタン距離1回分しか考慮されない最遠の点を「弾かれる最遠の点」と表現します)
まず、最適な点Pが最大2つの中央値に囲まれた長方領域上に含まれることを示します。これは1次元上に落として考えると考えやすいです。
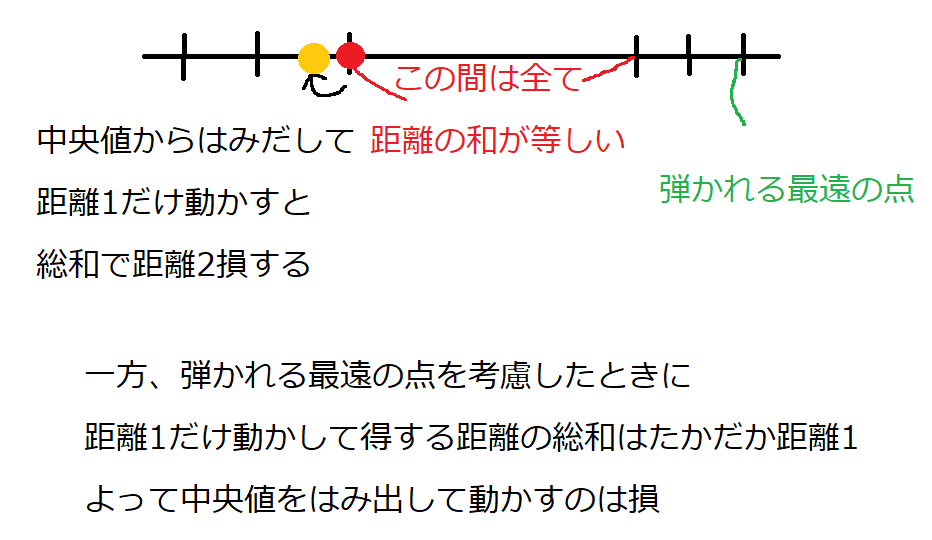
次に、最適な点は中央値同士で囲まれた長方領域の四隅のどれかになることを示します。これは目標と同値です。
ここで、ある点を通る2直線 y=x+C,y=-x+C(Cは定数)を使って議論します。
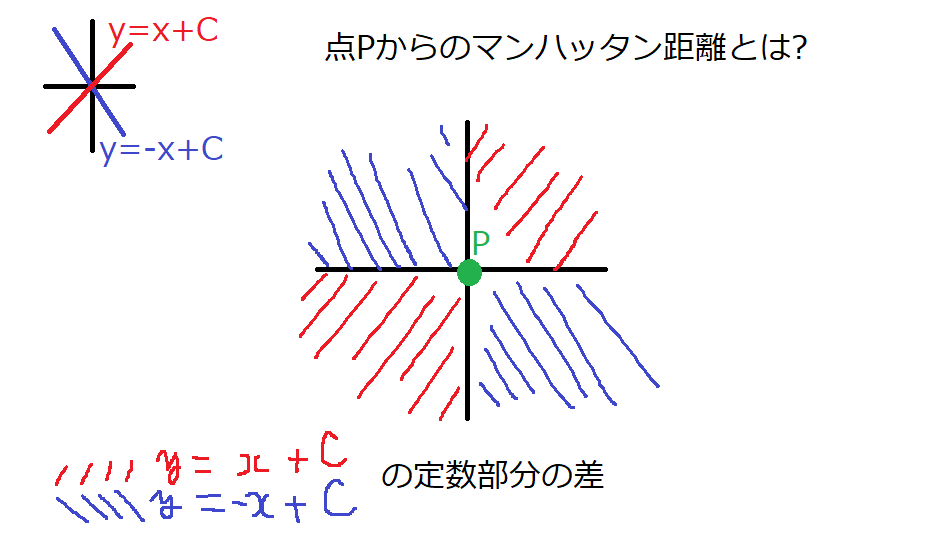
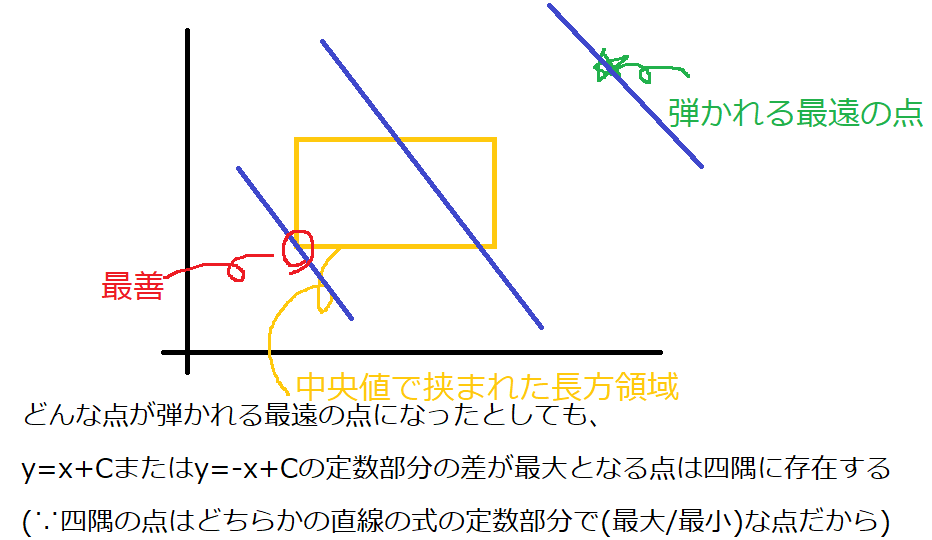
よって証明出来ました。(図証中心ですみません…)
あとは実装をすれば通ります。
https://atcoder.jp/contests/joi2011ho/submissions/4835990
Differ by 1 Bit(AGC031-C)
まず、答えが絶対にNOとなる場合を導きます。
操作回数の総合計は回で、これは奇数です。とすると、Aから奇数回操作をかけると立っているbitの本数の偶奇が逆転することがわかります。結局、AとBで立っているbitの数の偶奇が一致していては構築できない、ということがわかりました。
ここからは、AとBで立っているbitの本数の偶奇が異なるとして、その場合必ず構築可能なように話を進めていきます。
まず、N=3,A=4,B=3とします。
二進法で表すと、A=100,B=011となります。
まず、AとBで異なるbitをひとつ見つけます。これは必ず存在することはわかります。(Aの立っているbitの本数とBの立っているbitの本数の偶奇は必ず異なるので)
すると、それを前半と後半で固定したくなります。(図の赤丸のイメージ)
ので、これを前半と後半で固定します。(図の橙)
図での1の連続と0の連続のつなぎ目の部分に何か同じものを入れると、その間の編集距離がちょうど1bitになります。
ここで、ここには何を入れるのが適切でしょうか。
まず、AとBの間で固定したbitは異なるものであるということに留意します。
すると、AとBの残りの部分では立っているbitの本数の偶奇が一致します。(図の緑)
ここで、Aの残りの部分のうち、まだ確定していないbitをひとつひっくりかえしたものXを考えます。すると、これはAの残りの部分ともBの残りの部分とも立っているbitの本数の偶奇が異なります。(図の青)
すると、(図では下2桁について)、XをいわばA',B'とした1つ小さいサイズの問題がふたつ生まれます。これを、問題のサイズが1になるまで繰り返すと、全ての問題間で「確定したbitの集合はすべての問題についてどこかが相異なり、問題のサイズをひとつ落とす」を繰り返しているので、これによってできる順列は必ず問題文の条件を満たします。
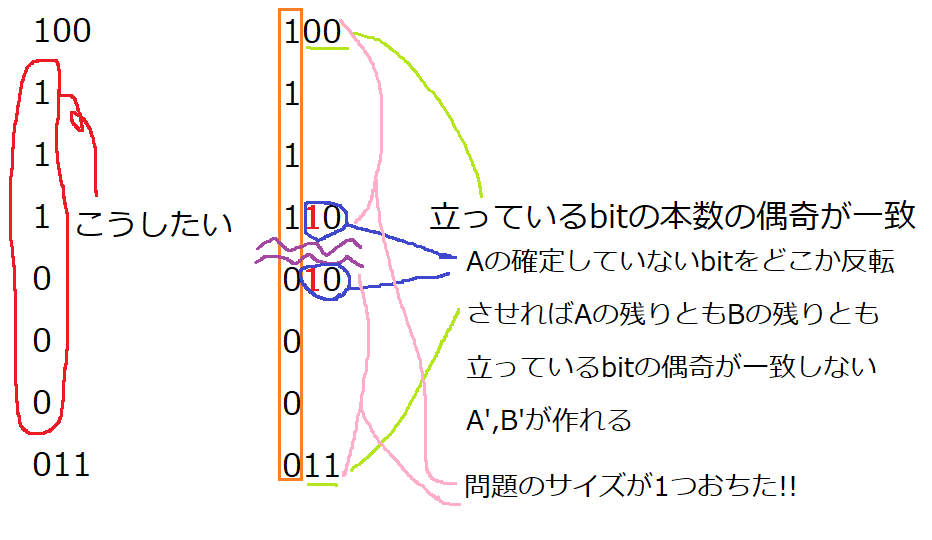
この流れを最後までやると、このような感じになります。
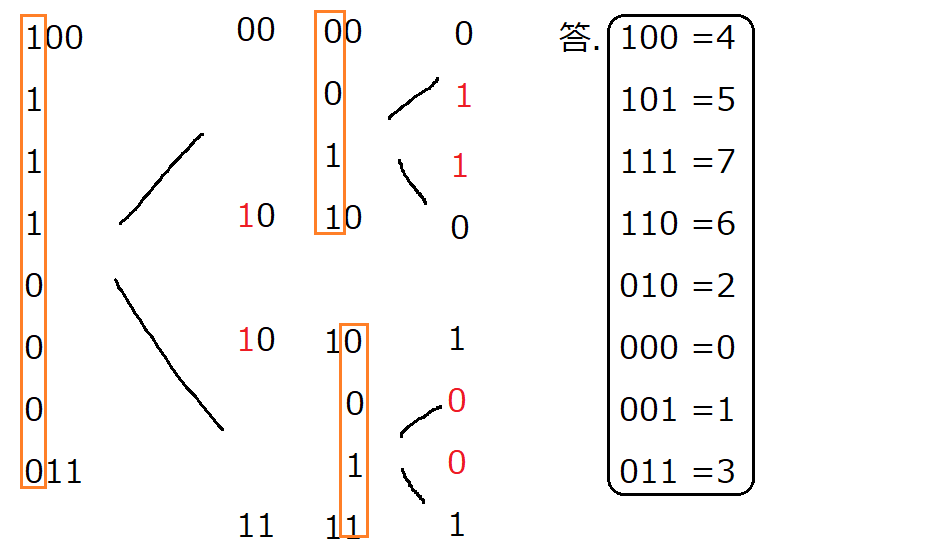
これを、bit演算を使って実行すると、この問題を解くことができます。
いくつか使うbit演算の例を示しておきます。
AとBの下からkbit目が異なるかどうか ((A>>(k-1))%2) != ((B>>(k-1))%2)
Aの下からkbit目を反転 A^=(1<<(k-1))