Distinct Boxes(AWTF2019-D)
この記事では、 D - Distinct Boxes の解説の内容をざっくり日本語に翻訳します。
(簡単のために空の箱を1つ作ることを認めておき、最後に解を-1するという前提で議論を行います。)
この問題では、「解 \(K\) を先に仮定して、\(K\) が実現可能かどうかは二分探索可能なので二分探索する」という方針をとります。
まず、図のような感じで、箱に入ったそれぞれの色のボールの数とxy座標系を対応させます。
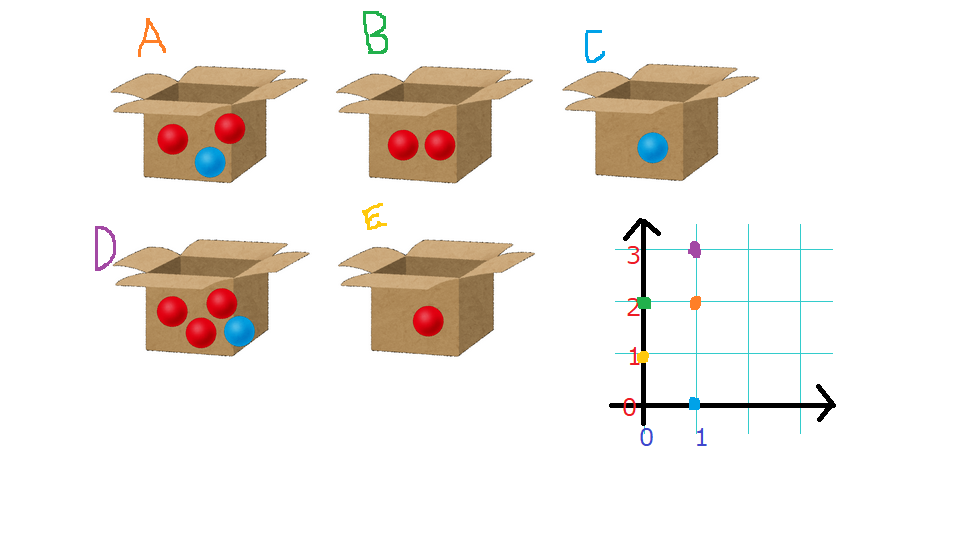
ここで、この平面に対してある直線 \(px+qy=C\) (p,q,Cは定数)を引くことを考えます。
図は \(2x+y=4\) を引いた場合の例です。
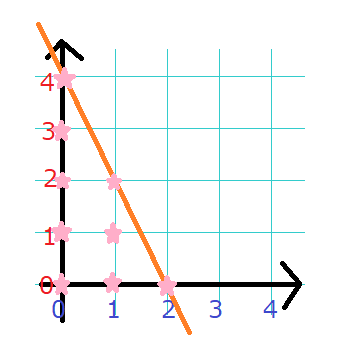
この直線の下に来る格子点に対応する箱をすべて作るということは、ある意味では「最適」です。
天下り的発想ですが、ここで \((B,R)\) についての解を座標平面上の対応する点に書き込んでみます。
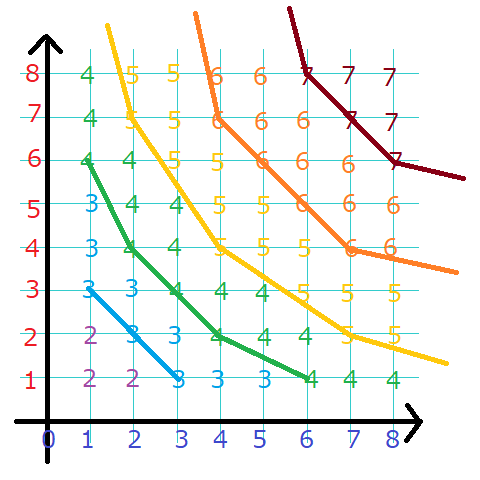
すると、図のような感じで、「解が \(K\) となる前線」は必ず上側凸包となるのですが、これを証明します。
まず、先ほどの \(2x+y=4\) の例を見てみましょう。

このときに、今 \(7\) 箱作りたいとしましょう。
今はこの直線を基準にとっているので、直線より下の \(6\) 点(に対応する箱)は作るのが最適です。しかし、 \(7\) 箱目を \((0,4),(1,2),(2,0)\) のどれにするかはこの間でのタイブレイクルールに依存します。そのことを掘り下げます。
今、 \(K\) 箱を作る時に引いた直線を \(3x+5y=C\) としましょう。
ここで、今 \(C=56\) で \((2,10),(7,7),(12,4),(17,1)\) の \(4\) 点がタイであるとし、既に \(K-2\) 箱作っていてここから \(2\) 点選ばねばならない状況だとします。
ここで、 \((2,10),(7,7)\) を選べば \(K\) 箱の合計が \(X,Y\) になるとします。
このとき、 \((7,7)\) を \((12,4)\) に交換した場合、 \((X+5,Y-3)\) でも \(K\) 箱作ることが出来ます。
さらに、 \(3x+5y=56\) より上側の点はまだ選ばれていないことにも注意すると、 \(\{(X,Y),(X+5,Y-3),(X+5,Y)\}\) の三角形領域にある点は全て \(K\) 箱作ることが可能です。
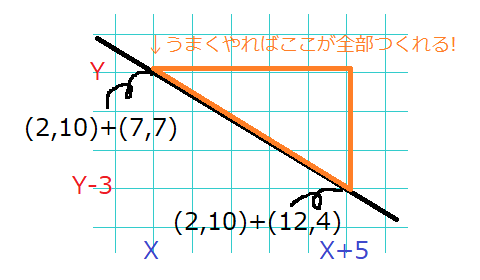
こんな感じで、線分の上サイドを次々に切り出す格好になります。(ここで、\((X,Y)\) より左側の点についてはたとえ直線の上サイドであっても \(K\) 箱作れるかどうかはまだわかっていないことに注意して下さい。)
これで、構成可能な点の上側凸包については \(K\) 箱作れることが分かりました。
ここで、万一前線の下側で \(K\) 箱作れるような場合が存在した場合、 \((X,Y)\) で構成可能なら \((X+1,Y),(X,Y+1)\) でも構成可能なことは元の問題に立ち返れば明らかです。そうなれば前線が全体的にずれ込むことがすぐに確認でき、またずれ込んだ点でも先ほどの上側三角形が作れるという議論が成立します。
よって、前線がちょうど上側凸包であることが示せました。
さて、これを利用して求解します。これは以下の3重の二分探索で実行可能です。
1. 解 \(K\) を仮定して二分探索(決め打ち二分探索)
2. 決め打った解に対して、\(K\) 箱作ろうとする場合の直線 \(px+qy=C\) の傾きを \(p+q=10^{10}+19\) などの条件を付けて二分探索(総和を十分大きい素数にとると全ての傾きを考慮できる)。傾き \((p,q)\) を与えると必要なボールの数 \((B,R)\) を返すようなものを作ることを考える。(これは下の 3. で行う)
二分探索はだいたい画像左側のような分岐で進みます。
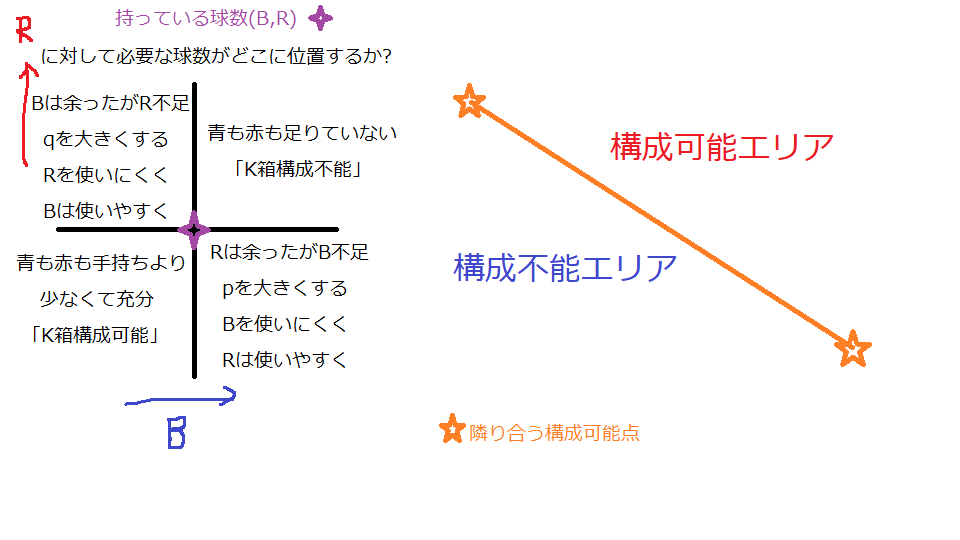
最後に、この二分探索が常に画像左側において左上か右下に入ってしまった場合。この場合は(凸包上で)隣り合い辺をなす構成可能点が求まっているので持っている球数を表す点が構成可能点同士を結ぶ点の上側か下側かを判定すればよく、これはベクトルの外積を利用すると可能です。
3. \(px+qy=C\) の \(C\) 部分を二分探索。直線の下側にある点の \((B,R)\) の総和は \(min(B,R) \le 2000\) までしか考慮しなくてよいことを利用すると求められる。