$xy$ 平面上の $N$ 点が与えられ、点 $i$ は $(x_i,y_i)$ にある。このとき、異なる $3$ 点は同一線上にない。
以下の通り $f(k)$ を定義する。
まず、点 $k$ を除いた $N-1$ 点の中から $4$ 点 $A,B,C,D$ を選択する。
このとき、 $A,B,C,D$ を結んで (凸でなくともよいが、非退化な) 多角形を構成することを考えるとき、点 $k$ を内部に含むことができるという。
$f(k)$ を、以上が成り立つ $4$ 点の組 $A,B,C,D$ (順序の違いは区別しない) の個数とする。
$\sum^{N}_{k=1} f(k)$ を求めよ。
制約
・$5 \le N \le 2500$
・$|x_i|, |y_i| \le 10^9$
まず、 包囲(ttpc2015-H) - physics0523's 精進ログ でも述べた通り、平面上のある点を内部に包含する冗長でない図形は「三角形」「包含したい点を対角線上に含む四角形」の $2$ 通りだけです。しかし、この問題の制約上 $3$ 点が同一直線上にないので、考えるべきは前者だけです。
次の場合分けを考えます。
- 選んだ $4$ 点の凸包が四角形である
- 選んだ $4$ 点の凸包が三角形である
実は、このどちらであろうと、以下の事実が成立します。
- もしこの $4$ 点が点 $k$ を包含するなら、選んだ $4$ 点の中から $3$ 点を選択した時に点 $k$ を包含する三角形が丁度 $2$ つ存在する。
以下のように図証します。
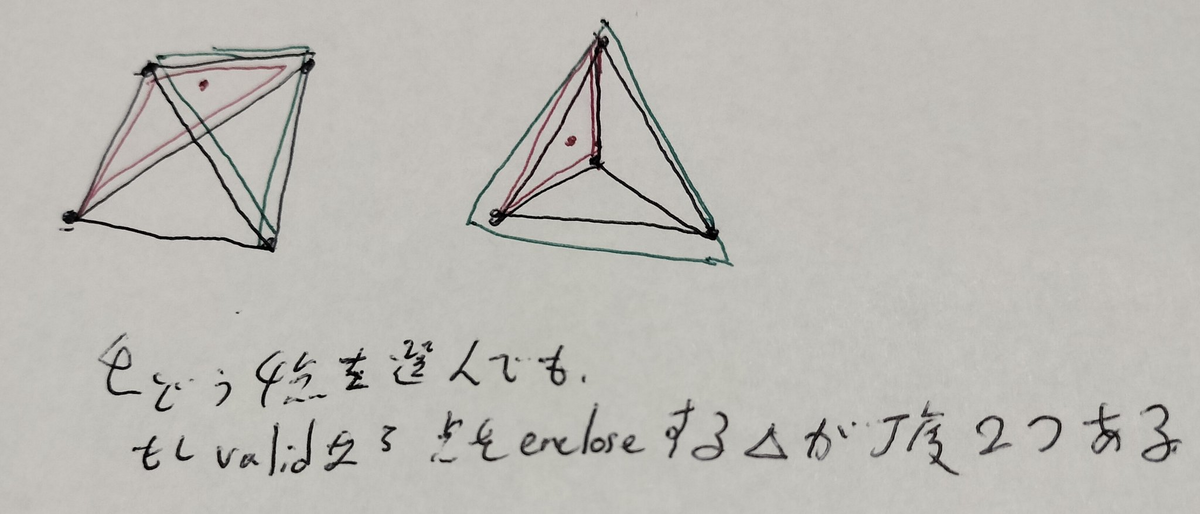
すると、主客転倒の考え方を使うと求めるべき値は以下のように言い換えられます。
- 全ての点 $k$ について、点 $k$ を包含する三角形の個数を数え上げ、それを $T$ とする。答えは全ての点 $k$ について $T \times (N-4)$ を足し合わせ、それを $2$ で割ったものとなる。
要するに、三角形と内包される点を選択したら、あと $1$ 点は自由に取れ、このもとでありうる全ての $4$ 点組を $2$ 度カウントするということです。
この時点で、求めるべきはある点を包含する三角形の個数を数える問題になりました。これは、偏角ソートを使うと解くことができます。具体的には次の通りです。
- 点 $k$ を包含しない三角形の個数を数える。この時、点 $k$ を中心に据えると三角形の点が反時計回りに $A,B,C$ と並ぶとする。すると、 $\angle AkC, \angle BkA, \angle C k B$ のうち丁度 $1$ つが $180^{\circ}$ 未満となる。 (これらの複数が $180^{\circ}$ 未満 となることはありえないことに注意されたい)
- 逆に、これが成り立たない時は三角形が必ず点 $k$ を包含する。
- この事実を使うと、尺取り法の要領で数え上げをすることができる。
以上より、この問題を時間計算量 $O(N^2 \log N)$ で解くことができました。
Submission #265114188 - Codeforces
どう点 $k$ を囲む $4$ 点を選んでも、その中で点 $k$ を囲む $3$ 点が必ず丁度 $2$ 組存在するという巧みな不変量を利用した美しい問題。