問題概要
$ n $ 頂点 $ m $ 辺の単純無向連結グラフが与えられる。
このグラフを $3$ 頂点 $2$ 辺のパスに分解できるか判定し、可能なら分解の一例を出力せよ。
$1 \le n,m \le 10^5$
まず $m\%2 = 1$ なら当然無理。こんな判定問題は単純なルールでもなければ $10^5$ 制約で解けるわけがないので、一旦 $m\%2 = 0$ の場合で絶対作れる読みで考える。
最初手として、「次数が少ない方からいい感じにやる」というような印象を受ける。そこで、問題を以下のように弱めてみる。
$n$ 頂点の木がある。 $n$ は奇数である (辺総数は偶数である)。この下で元の問題を解け。
木で解けなければ話にならない。同時に、木には「葉」とかいう次数 $1$ の頂点がある。これは現状の構築法上困りそうだ。
一旦次数 $1$ の頂点があったらそこからパスを適当に取るみたいなものをイメージして考察を進めつつ、さらに問題を弱める。
このグラフについて問題を解け。
葉は $1,4,5$ の $3$ 頂点である。葉 $1$ を最初に選ぶと上手くいきそうだが、葉 $5$ を最初に選ぶと $2 - 3 - 5$ というパスを取った時に詰む。この場合は $4 - 3 - 5$ というパスを取れば良いのだが、このように毎回よさげな頂点を選択するような方針は良くなさそう。(更に、変な取り方をするとグラフが非連結になって詰みかねない)
ここで、連結性が壊れた時のことを考えてみる。連結性が壊れても、両側の辺の総数が偶数になれば(仮定が正しければ)うまくいくはず。
ここで、(幸運にも)以下のような感じの木DPを思い当たった。

頂点 $1$ が根であり、各辺には「その辺以下にある辺の数の総和」が書かれている。
ここで、根から以下のことをすると、木の場合が解ける。
- 下に向かって伸びている辺のうち、奇数が書いてある辺同士でマッチングしていく。すると、その下の部分木には偶数個の辺が残る。
- もし辺がひとつ余ってしまった場合、その頂点とその親を結ぶ辺が余っているはず(現在見ている部分には偶数個の辺が残っているはず)なので、それとマッチングする。

先ほどの場合、以下のように分解できます。親を結んでいる辺とマッチングする場合は $3 - 6 - 10$ のパスのこと。
補足: この方法で辺が余ってしまうことはない。ある辺が余るためにはまずその辺が「今見ている頂点とその親とを結ぶ辺」になる必要があるが、この時「今見ている頂点以下にある辺の総数」が奇数になっているはず(今の連結成分には辺が偶数個あるので)なので、その辺は確実にマッチングに使われることになる。
では、一般グラフの場合について解いていきましょう。といっても、対処はそう難しくありません。
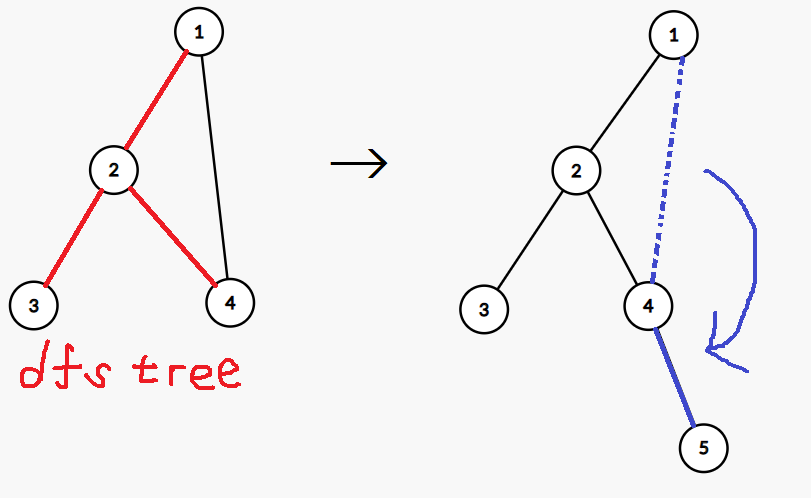
DFS木を適当にとってやり、後退辺を「その頂点から新たに適当に作った頂点に伸びる葉」として取り扱えば、木の場合に帰着できます。
こうして、この問題を解くことができた。
実装時、DFSしながら後退辺を記録する時に同じ辺を複数回使わないように注意する必要がある。
Submission #186704298 - Codeforces
むちゃくちゃ面白い、 2300diff なのに 2,3 日ほどかかってしまったのでメモ。
個人的には「問題をうまく弱めて、 $4$ 頂点でもしんどそうな例を見つけてどうにかする」という方針がまぁまぁよくハマってくれたのがお褒めな点。
