座標平面上のある凸多角形を構成する\(N\)点の点集合 \(A_1,A_2,...,A_N\)がある。
あなたはこの点集合に対して以下の\(2\)種類のクエリを合計で高々\(3N\)回問い合わせることができる。
- クエリ\(1\) : 三角形\(A_iA_jA_k\)の面積の\(2\)倍を尋ねる。
- クエリ\(2\) : \(\vec{A_iA_j}\times\vec{A_iA_k}\)(ベクトルの外積)の符号を尋ねる。返答が\(1\)のとき正、\(0\)のとき零、\(-1\)のとき負である。
どちらのクエリも尋ね方はt i j k(\(t\)は\(1\)または\(2\)のクエリ種別)であり、\(1 \le i,j,k \le N\)かつ\(i,j,k\)は相異なる必要がある。
この時、以下の条件を満たす要素が\(1,2,...,N\)である順列\(P=\{P_1,P_2,...,P_N\}\)を復元せよ。
- \(P_1=1\)
- \(A_{P_1},A_{P_2},...,A_{P_N}\)はこの順番で反時計回りに凸多角形を構成する。
なお、ベクトルの外積の定義はもとの問題文にもあるように、\(\vec{A}\times\vec{B}=A_xB_y-B_xA_y\)です。外積をスカラーとして扱うあれ。包囲(ttpc2015-H) - physics0523's 精進ログでも用いたものなので、詳しくは当該記事も参照。
とりあえずの発想としては、多角形のある\(1\)辺\(XY\)を特定した後、そこに他の頂点を加えてできた三角形の面積は加えた頂点の反時計回り順で見ると単調増加→単調減少となる…といったもの。(ちょっと図で線が混み入ってるのはご勘弁を。)
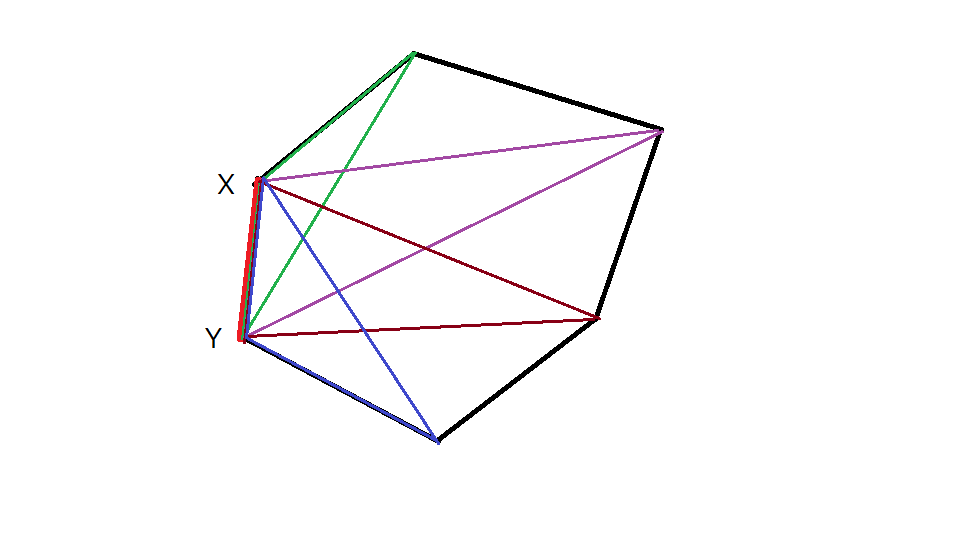
とりあえずある\(1\)辺\(XY\)がなんとかして特定できたとして話を進めます。
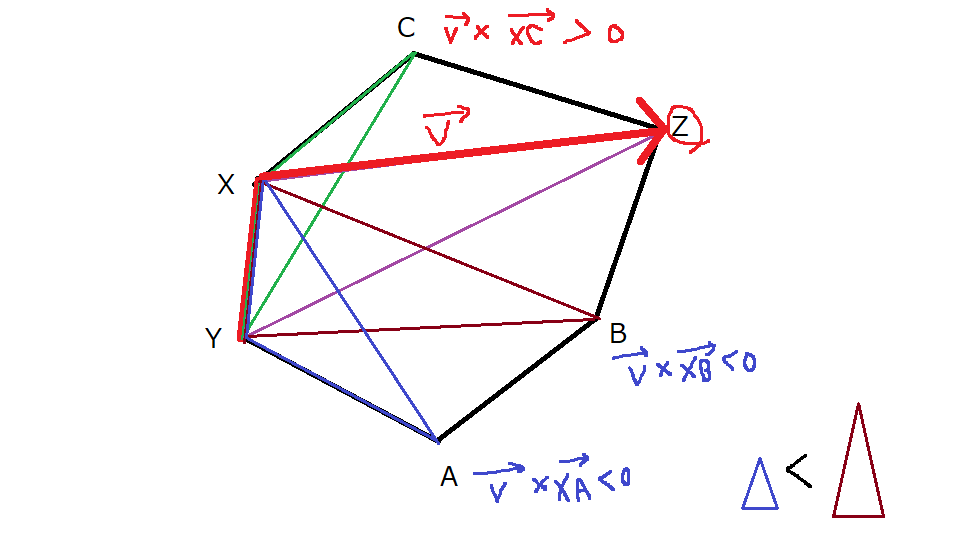
このとき、\(XY\)に加えて面積最大となる点を\(Z\)とします。
すると、\(\vec{XZ}\times\vec{XA_i}\)の正負で\(A_i\)が\(X\)から見て時計回り側にあるのか反時計回り側にあるのかがわかり、面積の(適切な)順でソートすると点集合が多角形を構成するように点をソートできます。以下の図のようなイメージです。
実装時は、\(i,j,k\)は相異なる必要があること、即ち、面積\(0\)となる質問をしてはいけないことや、同じベクトル同士の外積を尋ねてはならないことに注意してください。
さて、ここまで、面積の問い合わせと点がどちら側にあるかの判定でクエリを\(2N\)回弱使いました。
あと\(N\)回で多角形の\(1\)辺を特定します。
これは、以下のようなアルゴリズムで可能です。
- 適当な\(2\)点\(X,P\)をとり、それらを調査済みにする。
- まだ調査済みでない点が残っている場合、その点を\(Q\)とする。
- もし、\(\vec{XP}\times\vec{XQ}<0\)だった場合、\(P \leftarrow Q\)とする。
- \(Q\)を調査済みにし、2に戻る。
- 最終的な\(XQ\)は多角形の\(1\)辺である。
感覚的な証明は図のような感じです。\(N\)回程度の比較で最小値を求めている感覚に近いかも…?
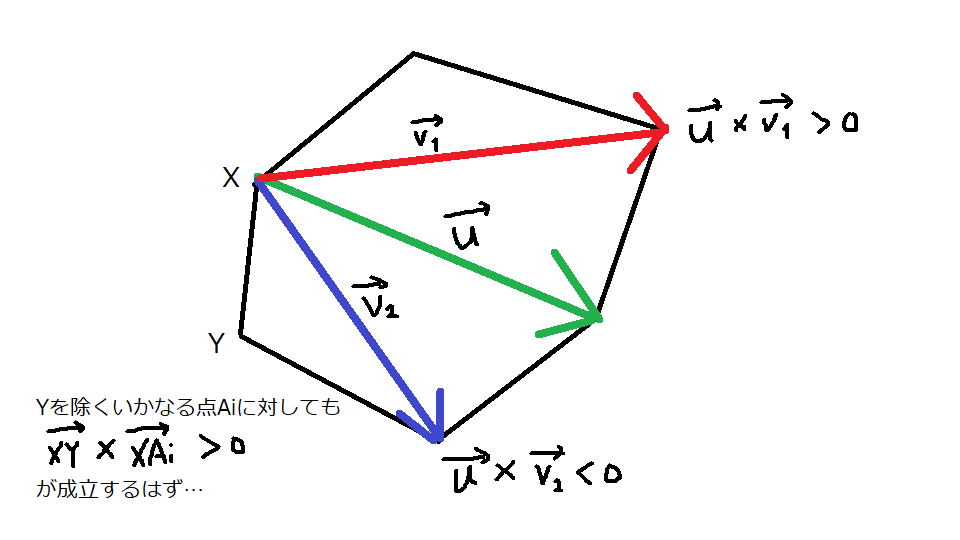
これを行うことにより、計\(3N\)回弱のクエリでこの問題が解けました。
実装の際、\(X=A_1\)としてやると問題の要求に沿った順列を復元しやすいです。
