私はこの問題を実験で刺し切りました。すみません。
事前情報として、この問題に挑んでいる話を通話で聞いて「互除法っぽい問題だな」ということは他の方から聞いてから取り掛かったので、それを参考にして解き(?)進めたということは書いておきます。
まず、明らかに $(A,B,C)$ の場合の解と $(A-B,B-B,C-B)=(A-B,0,C-B)$ の解は一致するので、 $(-P,0,Q)$ ( $P,Q \ge 0$ ) の場合について解ければこの問題が解けたことになります。(これを $f(P,Q)$ とおいておきます。)
$f(P,Q)$ を列挙した表が以下です。 (行/列 ともに 0-indexed)

簡単な場合として、以下を上から順の優先順位で処理しておきましょう。
$\min(P,Q) = 0$ のとき、 $\max(P,Q)=0$ なら $f(P,Q)=1$ 、そうでないなら $f(P,Q)=2$
$P=Q$ のとき、 $f(P,Q)=5$
$\min(P,Q) = 1$ のとき、 $R=\max(P,Q)$ として $f(P,Q)=5+R^2$
自明な性質ですが、 $f(P,Q)=f(Q,P)$ なので、 $P \le Q$ の場合が解ければよいことになります。
さらに、 $f(P,Q)$ の $P,Q$ が互いに素でない場合は、 $\gcd(P,Q)=g$ として $f(P/g,Q/g)$ に帰着できます ( $P,Q$ の少なくとも一方が $0$ みたいな時は無視してください)。なので、 $P,Q$ が互いに素でない場合の実験結果は消しちゃいましょう。

この表をぐっと睨みます。例えば $P=3$ をご覧ください。
$14$ $17$ -> $27$ $30$ -> $42$ $45$ -> $59$ $62$ -> $\dots$
これは $3$ 項間隔で $2$ 本の以下の数列が並んでいると推測できます。
- $14,27,42,59 \dots$ = 初項 $14$ 、初公差 $13$ 、階差 $2$ の階差数列
- $17,30,45,62 \dots$ = 初項 $17$ 、初公差 $13$ 、階差 $2$ の階差数列
(ここで階差数列という単語を使っているのは一般には大嘘です。ここでは公差を数列とみたときに等差数列となっているようなものを階差数列とし、公差を並べた数列の初項を初公差、公差を階差と呼ぶことにします。)
$P=7$ とかは互いに素な例が多いので調べやすそうです。 $7$ 項間隔で
- $54,107,162$ = 初項 $54$ 、初公差 $53$ 、階差 $2$ の階差数列
- $39,74,111$ = 初項 $39$ 、初公差 $35$ 、階差 $2$ の階差数列
- $42,77,114$ = 初項 $42$ 、初公差 $35$ 、階差 $2$ の階差数列
- $47,82,119$ = 初項 $47$ 、初公差 $35$ 、階差 $2$ の階差数列
他にもいろいろ調べてみると、全部 $P$ 項間隔で取り出した時に階差が $2$ の階差数列になるので決め打ってよさそうです。
ここで、ざっくり以下のような方針が立ちました。
$R=Q\%P$ とおいて、 $f(P,R),f(P,P+R)$ が分かれば階差数列の情報が全て得られるので、再帰的にやれるのでは?
とりあえずこの再帰を実装したんですが、以下の問題が発覚しました。
例えば $f(4,5)$ を求めようとすると、 $f(4,1),f(4,5)$ を求めることになり、 $f(4,5)$ について無限再帰になる。
現場からは以上です。ここまでお付き合い頂きありがとうございました。[終]
とも言ってられないので、どうにかします。
$R=Q\%P$ とおいて、 $\color{red}{f(P,-P+R)},f(P,R)$ が分かれば階差数列の情報が全て得られるので、再帰的にやれるのでは?
なんかヤバいことが書いてあります。 $f(4,5)$ が求められないからと言って $f(4,-3)$ を考えようとしています。
多分換言した方がわかりやすいですね。階差数列の「第 $1$ 項」と「第 $2$ 項」が出せないなら、「第 $0$ 項にあるべき数字」と「第 $1$ 項」が出せれば良いです。
ここでさらに、次の実験を行います。
「$f(P,R)$ ごとに、 $f(P,R)$ を階差数列の第 $1$ 項とした時に第 $0$ 項にあるべき数字を求める」、すなわち、 $f(P,R)-(f(P,P+R)-f(P,R)-2)$ を $(P,R)$ の組ごとに列挙した表を書いてみましょう。(今回は行/列ともに 1-indexed で表を書いています)

今回も、いったん $R \le 4$ の場合までは自明であるとしておきましょう。 $R=1$ のとき $3$ 、 $R=2$ の場合は $6$ 、 $R=3$ の場合は $9$ 、 $R=4$ の場合は $14$ です。
$R=5$ 以降の数列、どこかで見たことありませんか?
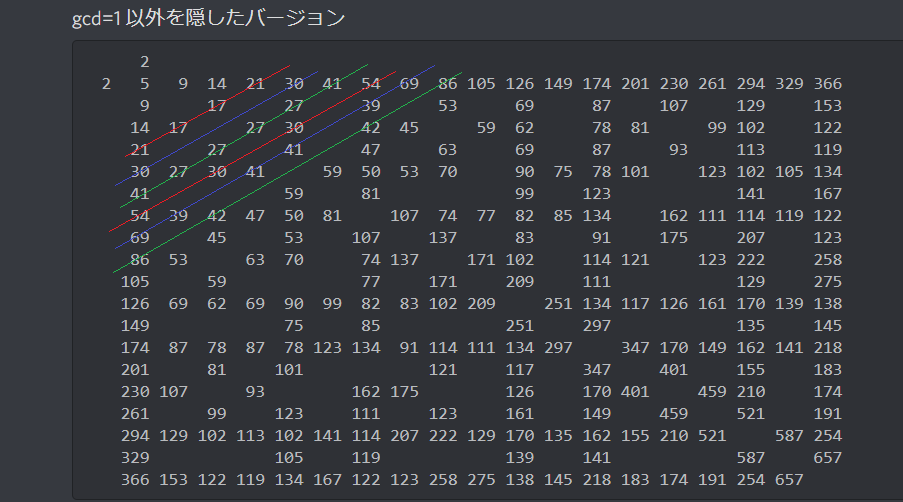
そうです! $f(P,Q)$ の数表を斜めに眺めたもの(を何度も繰り返し貼り付けたもの)です!さらに、この表では「表を斜めに眺める」=「総和が一定」です。
これより、 $S=(P-R)\%R$ とおくと、 $f(P,-P+R) = f(S,R-S)$ としてやればよいことになります。(いくつかこの値を手で試すと推測できるのですが、 $(S,R-S)$ は $(P,Q)$ から互除法を何ステップか進めた時のペアになることが予想でき、この後の大胆予想の $2$ 番目の項目は実際に恐らく正しいです。)
ここまでの考察と、サンプルが十分高速に通ったことによる以下の $3$ つの大胆予想を使えば、この問題を通すことが出来ます。
- やってる操作が互除法なので、無限再帰になることはもうない(これがないとこわれます)
- やってる操作が互除法なので、メモ化再帰で $f$ を求めていく際に通る $(P,Q)$ の組の数はどうせ $O(\log(P+Q))$ 個とかそんなところになりそうだ(これがないと最悪 $O(PQ)$ とかになります)
- やってる操作が互除法なので、 最初に $P,Q$ を互いに素なように正規化してしまえばそれ以降は $f$ を求める道中で $\gcd$ を取って両項を割るような操作が必要なくなるはず(高速化に必要です)
Submission #34625499 - AtCoder Grand Contest 057
実験数列にらめっこ、最高!w
といっても何もこの解法(?)をストレートに出したなどということはなく、いろんな実験の試行錯誤を経てここに至っています。色んな数列の階差を取ったり何かしらの規則がないか多くの予想を立てて最終的にここに至りました。
とはいえパッと見て「等差数列」「階差数列」「その他規則性のありそうな数列」が見えればそこに実験チャンスが色濃くあるのは確かです。但し、実験ばかりに凝り固まるのはもちろん危険なのでご注意を。