Triangle
おふざけはこのへんにしておきましょう。
問題概要
平面上の $n$ 点 $(x_i,y_i)$ が与えられる。
この中の $3$ 点を選んで、選んだ点を結んだ三角形の面積を $S$ と出来るか判定し、可能ならそのような三角形をひとつ復元せよ。
$3 \le n \le 2000$
$|x_i|,|y_i| \le 10^9$
$1 \le S \le 2 \times 10^{18}$
与えられる点からどの $3$ つを選んでも同一直線状に乗らない
$O(n^3)$ は自明。気合いで二乗系に落とす。
ここで、三角形の等積変形に思いを馳せる。
等積変形とは、三角形のある辺 $E$ を選んだ時にそこに含まれない点を $E$ に平行に動かしても面積が変わらないことを利用して三角形の面積を変えずに変形すること。図中の赤い点を直線 $l$ 上で動かしていく感じ。
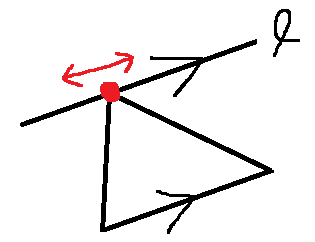
つまり、底辺を決め打った時に適当に面積が $S$ となる点を (底辺の両側それぞれに $2$ 通り) 取ってやれば、そこから底辺に平行な直線を伸ばしてその上に $3$ 点目が来るはず。こんな感じの方針で $3$ 点目を賢く求めれば $O(n^2 \times f)$ ( $f = o(n)$ ) で解けそう。なので、 底辺を固定する を方針の軸として進める。
ある底辺を決め打った時に、どのように $3$ 点目を探せば良いだろうか?
当然 $O(n)$ かけるとできるが、もっと賢くやりたい。ここで、先ほどの等積変形のイメージを利用する。
底辺を決め打った時に、「ある直線より上」か「ある直線より下」か、はたまた「ある直線上にある」かを区別することになる。もっと言えば、三角形の底辺を決め打った時に「高さ」順でソートできていれば $f=O(\log n)$ で $3$ 点目を探索できる。
ここで、「高さ」とは何かをもう少しはっきりさせておきましょう。三角形の底辺を延長した直線が $y=ax+b$ であって $3$ 点目が直線 $y=ax+b+C$ に乗る時、 $C$ が「高さ」と思うと良いでしょう。
「底辺」と「ある $2$ 点の高さの関係」の関係について調べてみましょう。
図のように底辺と平行な直線の偏角を徐々に大きくしていくと、 $2$ 点を結ぶ直線を境に上下関係が反転します。

ここで、賢いことを思いつきます。
「底辺を偏角順に舐める過程で、各点を高さ順にソートした配列 $A$ を保持していくことを考えると、ある辺が出てきたときに配列 $A$ 上でもその $2$ 点をswapすれば配列 $A$ を正しく更新できる」ということに気づきます。 (平行線が複数ある場合があるが、どの順で更新してもよい + 同一直線上の $3$ 点がない ため、ここで困ることはない)
このアイデアを実装すると、底辺を固定した時に配列 $A$ から目的の点を二分探索を利用して $O(\log n)$ で見つけることが実際に可能となり、最終的な時間計算量 $O(n^2 \log n)$ を達成できます。
Submission #195739559 - Codeforces
事前情報としてCD逆転を把握してたとはいえ、ばちゃ中にこれ通し切ったの褒めて欲しい。あと 復元忘れで1ペナ → ジャッジで YesNo の大小文字吸収がかかってない時代の問題みたいでそれで1ペナ → AC で暴れそうになった。